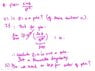Procedure to test pole and its order

[DrMath]

Homework Statement

I have a query - regarding the procedure to test pole.
As attached. pse find.

so, z is not a pole but a Removable Singularity?

NEXT, if z is not a pole (which is true for above) - no point testing for the order of the pole right?

Homework Equations

The Attempt at a Solution

 

[jmb]

The attached problem is not a removable singularity. If it were then the limit of your function multiplied by $(z-z_0)$ would tend to zero as $z$ tends towards the pole at $z_0$ (in your case $z_0=0$).

As for testing the order of the pole, you can think of a removable singularity as just a pole of order zero, in which case checking that it is a removable singularity and checking for the order of the pole are the same task!

 

[DrMath]

Hi,

So z=0 is actually a suspected pole just by looking at the question.

However - it is not a real pole right?
Because my test of pole procedure determines it is not a pole.
So i thought it is a Removable Singularity - here confuse!

From my understanding from you; it is a removable singularity if we take the limit of
z tends to 0 (pole) --- from my attachment i raise it to the power of 15. Is this not correct ?

 

[jmb]

So z=0 is actually a suspected pole just by looking at the question.

Yes the denominator of your fraction is zero there, so you need to test for a pole at $z=0$.

However - it is not a real pole right?
Because my test of pole procedure determines it is not a pole.

No it is a real pole. As I said in my previous post, if the limit of the function multiplied by $z$ as $z\rightarrow 0$ was zero then it would be removable.

You have multiplied by $z^{15}$. That's not the same thing!

From my understanding from you; it is a removable singularity if we take the limit of
z tends to 0 (pole) --- from my attachment i raise it to the power of 15. Is this not correct ?

No it's not at all correct.

The order of a pole at some point $z_0$ is defined as the smallest integer $m$ you can find such that:
$$\lim_{z\rightarrow z_0}{\left[\left(z-z_0\right)^{m+1}\,f\!\left(z\right)\right]=0$$

If $m$ is zero then it is called a removable singularity. (If $m$ is less than zero then it's not a pole at all)

Given this, can you now see what the order of your pole is?

PS My initial post contained a mistake in my description of the limit you are supposed to take, which probably hasn't helped with your confusion! I'll edit it and fix it...

 

[HallsofIvy]

$$lim_{z\to 0}\frac{sin(z)}{z}= 1$$
so $sin(z)/z^{15}= (sin(z)/z)/z^{14}$ you can tell the order of the pole from that.

 

[DrMath]

its pole of order 14; z=0

 

[jmb]

its pole of order 14

Yup, that's right.

 

[DrMath]

If this qn is extended to use the residue theorem directly...
the residue of the function, z=0: i would need to differentiate 13 times?

 

[jmb]

Yes, but it's not just the function you need to differentiate. You should have this in your textbook already, but if not look here:

http://en.wikipedia.org/wiki/Residue_(complex_analysis)#Limit_formula_for_higher_order_poles

 

[DrMath]

i find it very tedious to work out 13 times...

 

[jmb]

Keep going! You've differentiated twice, so you need to do another eleven. If you keep regrouping like terms together it shouldn't end up too difficult. Also don't forget the factorial multiplying the final answer...

 

[DrMath]

But as i proceed...
Say at the 3rd time.. it becomes (as attached).

Hmm.. so i assume after up to 13 times differentiated; is should get things like:

- K sin (2z) / z^14 + ...+ ...+ - (Last temr -ve here) ------ by pattern matching.

(well, if i take limit term by term; this term gives me 'undefined').
So not sure am i on the track?

 

[DrMath]

attached

 

[jmb]

Sorry for slow reply, been rather busy.

The limit only appears undefined because you are applying it term by term as you have written it. You need to group all the coefficients of $1/z^2$ together (and similarly $1/z^3$, etc. etc.). Then L'Hopital's rule or judicious Taylor expansion of sin and cos should give you a finite limit. So keep on with the differentiating --- you've only done 3 out of 13 so far!

If you really can't handle differentiating that many times (although it really shouldn't be that difficult for this function) then you could get at the residue by instead expanding the function in terms of its Laurent series --- your textbook/lecture notes should cover that.