Projected Area of a Cone in Electric Field Calculation

[Tanya Sharma]

Homework Statement

Homework Equations

Flux = ∫E.ds

The Attempt at a Solution

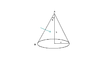
I need to get the projection of cone on a plane perpendicular to the electric field . The area thus obtained when multiplied by electric field would give the flux .

I am not able to imagine the projected area .Is there a systematic way to calculate the projected area ?

I would be grateful if somebody could help me with the problem .

 

[mooncrater]

Hint: You can convert the electric field into components parallel and perpendicular to the base of the cone.

 

[TSny]

Spoiler: Too much help?

Is the flux you're looking for related to the flux through the blue and yellow shaded regions shown below?

[EDIT: Sorry, ignore this post! I didn't visualize it carefully enough. Attached diagram was deleted to avoid being misleading .]

 

[TSny]

Consider a patch of area as shown. Can you express its unit normal vector $\hat{n}$ in terms of the angles $\theta$ and $\phi$ and the $\hat{i}, \hat{j}, \hat{k}$ unit vectors?

 

[Tanya Sharma]

Hint: You can convert the electric field into components parallel and perpendicular to the base of the cone.

Very nice ! Thank you .

 

[Tanya Sharma]

Consider a patch of area as shown. Can you express its unit normal vector $\hat{n}$ in terms of the angles $\theta$ and $\phi$ and the $\hat{i}, \hat{j}, \hat{k}$ unit vectors?

Sorry . Could you please elaborate a little .

 

[TSny]

The unit normal vector is parallel to the area vector of the patch. So it can be used to help express the flux through the patch.

I'm not sure I'm interpreting the original question properly. "Find the magnitude of the flux that only enters the cone's curved surface. Do not count the outgoing flux."

I interpret that to mean that for a patch of area on the curved surface where the flux is outward rather than inward, then we do not count that flux. Is this the way you also interpret it?

 

[Tanya Sharma]

Yes .

 

[TSny]

OK, good. If you had an expression for $\hat{n}$, how could you use it to determine if a patch of area has inward flux or outward flux?

 

[Tanya Sharma]

Sign of $\vec{E} \cdot ds\hat{n}$ determines whether flux is positive or negative . $ds$ is the area element of the differential element .

 

[TSny]

Yes. That's why I think it's a good idea to find vector expressions for $\vec{E}$ and $\hat{n}$.

 

[Tanya Sharma]

But how do I calculate $\hat{n}$ ?

I haven't done something like this before . Does it involve spherical coordinates and double integrals ? Could you give some relevant web link ?

 

[TSny]

It's similar to working in spherical coordinates. If you projected $\hat{n}$ onto the xy plane, how long would this projected vector be in the xy plane (expressed in terms of $\theta$)? How can you express the x and y components of this projected vector in terms of $\theta$ and $\phi$?