Projectile Motion football kicker

[Dante Tufano]

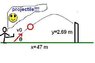
1. A football kicker can give the ball an initial speed of 26 m/s. He is 47 m from the goalpost which has a crossbar 2.69 m high.
(a) What is the smallest angle of elevation that he can kick the football and score a field goal?
1°

(b) What is the largest angle of elevation that he can kick the football and score a field goal?
2°



2. x-xo=(vocos(theta))t
y-yo = (v0sin(theta))t-(1/2)gt^2
vy=vosin(theta)-gt
vy^2=(vosin(theta))^2-2g(delta y)
delta y = (tan(theta))(delta x) -(g(delta x)^2)/(2*(vocos(theta))^2)
v^2=v0^2-2g(y-y0)


3. I honestly have no idea how to solve this. I tried to plug my values into the equation v^2=v0^2-2g(y-y0) to get some idea of what the velocity at the goal would be, but I'm not even sure if I need that information or what to do afterwards. Please help give me some direction.

 

[ehild]

A drawing could give you hints... The ball has to cover the distance of 47 m, and when x=47 m it should fly lower then the crossbar.

One more hint: To solve the equation for theta, you can use that cos^(theta) = 1/(1+tan^2(theta))

 

[Dante Tufano]

So.. could I use the Pythagorean theorem to figure out the angle? I'm still not quite sure how to discern the largest possible angle from the smallest.

 

[rl.bhat]

delta y = (tan(theta))(delta x) -(g(delta x)^2)/(2*(vocos(theta))^2)

I will rewrite the above equation as

y = x*tanθ - 1/2*g*x^2/vo^2*cos^2(θ)
y = x*tanθ - 1/2*g*x^2*sec^2(θ)/vo^2
y = x*tanθ - 1/2*g*x^2*[1+tan^2(θ)]/vo^2
Substitute the values and solve the quadratic.
One value will be a smaller angle and the other value will be a larger angle.

 

[Dante Tufano]

Awesome, I plugged in the values and got angles of 67.9 degrees and 25.4 degrees, which are correct! Thanks a ton guys, much appreciated. Any advice on how to know which equation to manipulate?

 

[ehild]

First: Try to visualize the problem. Here: imagine you want to score a goal. (see my beautiful picture drawn specially for you For that, the ball has to go far away but not too high. Draw a figure to see what this mean, and how your drawing is related to the data given in the problem. From the picture, try to find out what part of Physics describes the situation. Here: it is projectile motion. Find the equations. You are given the horizontal and vertical distance, use the equation for y in terms of x and theta.

ehild

 

[Dante Tufano]

Hahaa, lovely picture, I think I get it now. Thanks a ton!