Projectile Motion Up An Incline Plane

[abhikesbhat]

Homework Statement

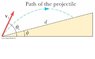
A projectile is fired up an incline (incline angle φ) with an initial speed vi at an angle θi with respect to the horizontal (θi > φ). (a.) Show that the projectile travels a distance d up the incline, where

d = 2*vi^2*cosθi*sin(θi-φ) / g*cos(φ)^2

(b.) For what value of θi is d a maximum, and what is the maximum value?

Homework Equations

The Attempt at a Solution

Ok I am back and unbelievably got part a, but I have no idea how to do part b. I know 45 is the way to get maximum range, but I don't think that is the right angle, because we want to maximize x^2+y^2. Any help would be appreciated!

 

[abhikesbhat]

Here's a picture.

 

[ideasrule]

You have an equation relating d, which you want to maximize, with θi. It is:
d = 2*vi^2*cosθi*sin(θi-φ) / g*cos(φ)^2

Do you know calculus? If you do, just derive d with respect to θi, set the derivative to zero, and solve for θi. It shouldn't be too hard if you remember a few trig identities, like sin(θi-φ)=sin(θi)cos(φ)-sin(φ)cos(θi).

If you don't know calculus, try to use trig identities to rearrange the formula for d so that it's easy to identify the maximum. Remember that vi and φ are constants, so the only part you need to maximize is cosθi*sin(θi-φ). This is much harder mathematically than using calculus; I can't immediately see how you would go about manipulating cosθi*sin(θi-φ).

 

[abhikesbhat]

Ah this derivative is too hard for me to get. I'll try your second way. Thank you.

 

[ideasrule]

The calculus way is actually very simple:

Derive cosθi*sin(θi-φ), because everything else contains only constants. Use the product rule and you'll get cosθi*cos(θi-φ)-sinθi*sin(θi-φ). Recall that cos(a+b)=cos(a)cos(b)-sin(a)sin(b), so:

cosθi*cos(θi-φ)-sinθi*sin(θi-φ)=cos(2θi-φ)=0

What must 2θi-φ be in order for cos(2θi-φ) to be zero?

Without using calculus:

cosθi*sin(θi-φ)=cosθi*(sinθi*cosφ-sinφcosθi)
=cosθi*sinθi*cosφ-sinφ*cos^2 θi
=cosθi*sinθi*cosφ-sinφ(cos(2θi) +1)/2, since cos(2θi)=2cos^2 (θi) - 1
=1/2 sin 2θicosφ - 1/2 sinφcos(2θi) - 1/2 sinφ
=1/2 (sin 2θicosφ-sinφcos(2θi)-sinφ)
The factor 1/2 can be neglected because it's a constant; so can sinφ for the same reason. Our job now is to maximize sin 2θicosφ-sinφcos(2θi), which can be rewritten as
sin (2θi-φ). The maximum possible value of a sine function is 1, so sin (2θi-φ)=1. What must 2θi-φ be?
Make sure that your answers for the calculus and non-calculus methods agree!

 

[abhikesbhat]

Ok I got θi=45+φ/2. Thank you.