kylinsky
- 5
- 0
1. The derivation
In a 3-dim space,a particle is acted by a central force(the center of the force fixed in the origin) .we now take the motion entirely in the xy-plane and write the equations of the motion in polar coordinate
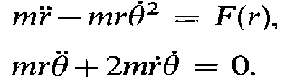
how can i derive from these equation that
T(kinetic energy)+V(potential)=E=
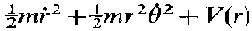 ?
?
(sorry for my poor english)
In a 3-dim space,a particle is acted by a central force(the center of the force fixed in the origin) .we now take the motion entirely in the xy-plane and write the equations of the motion in polar coordinate
how can i derive from these equation that
T(kinetic energy)+V(potential)=E=
(sorry for my poor english)