dk123
- 2
- 0
- Homework Statement
- How do I prove that a projectile in a two-dimensional trajectory motion comes to rest in a finite distance when v>0
- Relevant Equations
- Projectile Motion Equation
equation of motion :
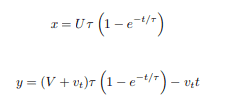
while
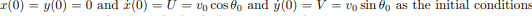
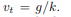
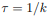
while
Attachments
Last edited: