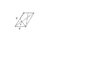kpollock2
- 1
- 0
Homework Statement
Ok, this is actually an assignment from my calc III class but it involves vectors so I was hoping I could get some help here.
The problem is There are two vectors A and B that make a parallelogram. I have to prove that when two line segments are drawn from a vertice from the vectors that bisect the vectors on the other side of the parallelogram the line segments will trisect the diagonal between the vectors. One of the tri-sections is labeled vector C. I am attaching a picture that I drew in paint which I think illustrates the problem. If it doesn't then It is how I understood it and that might be why I am having trouble to begin with. I have scribbled down a few things that I know are true, but I am really having a problem getting started.
Homework Equations
Relevant info is all rules pertaining to vectors and geometry and trig. I'm sure I'm just overlooking something simple.
The Attempt at a Solution
I have tried starting with the assumption that A+B= 3C
1/2A+B= one of the line segments
A+ 1/2B= the other line segment
these are things that I think maybe I need to assume to be true but I honestly have no idea where to start. Could someone please point me in the right direction? The diagram is really bad btw and not to scale, (like I said, I drew it in paint).