Prove PM is Diameter in ΔABC with ∠A = 90°

[Lukybear]

Homework Statement

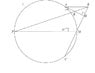
In ΔABC, ∠A = 90°, M is the midpoint of BC and H is the foot of the altitude from A to BC. A circle l is drawn through points A, M and C. The line passing through M perpendicular to AC meets AC at D and the circle l again at P. BP intersects AH at K.

Prove that PM is diameter.

The Attempt at a Solution

No idea how to do at all. Any help would be appreciated, as this is part 1 of a long question.

 

[G037H3]

okay, but what are you trying to figure out?

 

[Lukybear]

Opps sorry. I want to figure out that PM is the diameter

 

[Lukybear]

Have found solution but need further help! Here is my attempt:

Found PM is diameter of circle l, Triangle MCD similar to Triangle MPC, Triangle DMB similar to Triangle BMP, Angle DBM = Angle ABK.

Prove AK = KH, (using similar triangles or otherwise)

 

[zgozvrm]

There seems to be a lot of extraneous information here. To prove that PM is a diameter of circle l[/tex], all you need to do is note that you are given a right triangle (\triangle ABC[/tex]) with M as the midpoint of BC. Therefore, D is the midpoint of AC (which can be shown since \triangle ABC[/tex] is similar to \triangle DMC[/tex]). AC is a chord to circle l[/tex] and since D is the midpoint of that chord, PM has to be a diameter.