Lukybear
- 8
- 0
Homework Statement
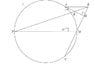
In ΔABC, ∠A = 90°, M is the midpoint of BC and H is the foot of the altitude from A to BC. A circle l is drawn through points A, M and C. The line passing through M perpendicular to AC meets AC at D and the circle l again at P. BP intersects AH at K.
Prove that PM is diameter.
The Attempt at a Solution
No idea how to do at all. Any help would be appreciated, as this is part 1 of a long question.
Attachments
Last edited: