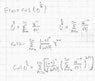Proving Essential Singularity at z=0: Using Taylor Series Method

[asi123]

Homework Statement

Hey guys.
I need to show that this function has an essential singularity at z=0.
I used Taylor series to get what I got, which is a series inside a series...
And I can't see how am I suppose to show it from here.
Any ideas guys?

Thanks.

Homework Equations

The Attempt at a Solution

 

[statdad]

Without seeing the result, or the original function, it's difficult to say what is right and what isn't.

 

[asi123]

Without seeing the result, or the original function, it's difficult to say what is right and what isn't.

Sorry

 

[Mark44]

Did you mean to write f(z) = cos(e^(1/2))? If so that's a constant function.

I'm having a hard time reading your writing, as your e looks like a cross between an e and a u. Is that thing in the numerator of the exponent on e the digit 1?

 

[HallsofIvy]

I think it is e^{1/z} not e^{1/2}.

Yes, write out the Taylor's series for e^x and replace x with z^-1 as you have done. Now, what is the definition of "essential singularity"?

 

[asi123]

I think it is e^{1/z} not e^{1/2}.

Yes, write out the Taylor's series for e^x and replace x with z^-1 as you have done. Now, what is the definition of "essential singularity"?

The Laurent series of f(x) at the point a has infinitely many negative degree terms, the thing is, how can you see that trough this series inside a series?

Thanks.

 

[HallsofIvy]

Oh, you have cos(e^1/z). I was only looking at your first e^1/z.

Well, e^1/z already has an infinite number of negative exponents. Certainly one of the coefficients will cancel out.