Swatch
- 88
- 0
Hi. I have a homework problem I've been trying to solve for three days I think.
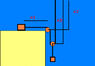
There is a block that lies on a horizontal table with mass = m1 it is connected to a cord which goes over a pulley on the edge of the table. The cord goes down and around another pulley (lets call it p2) the cord goes up again and is connected to a ceiling a little higher than the table. To the p2 pulley there is connected another block with mass= m2. The m2 block has an downward acceleration a2, and the m1 block has an acceleration a1,to the right . The problem is to find these accelerations a1 and a2 in terms of m1, m2 and g.
I hope you will be able to picture this.
So far my work is this:
The string connected to block m1 has tension: T=m1a1
For block m2 : m2*g - 2*T = m2*a2
The right answers are :
a1 = 2*m2*g/(4*m1 + m2)
a2 = m2*g/(4*m1 + m2)
I have no clue how to reach to this conclusion, could someone please give me a hint.
There is a block that lies on a horizontal table with mass = m1 it is connected to a cord which goes over a pulley on the edge of the table. The cord goes down and around another pulley (lets call it p2) the cord goes up again and is connected to a ceiling a little higher than the table. To the p2 pulley there is connected another block with mass= m2. The m2 block has an downward acceleration a2, and the m1 block has an acceleration a1,to the right . The problem is to find these accelerations a1 and a2 in terms of m1, m2 and g.
I hope you will be able to picture this.
So far my work is this:
The string connected to block m1 has tension: T=m1a1
For block m2 : m2*g - 2*T = m2*a2
The right answers are :
a1 = 2*m2*g/(4*m1 + m2)
a2 = m2*g/(4*m1 + m2)
I have no clue how to reach to this conclusion, could someone please give me a hint.