Pulley free body question - what am I doing wrong?

[johnschmidt]

Homework Statement

Note that the FAQ is not clear if I am required to use LaTeX for formatting formulas. I have not used LaTeX, but I will retype my question if I am violating the rules. Please let me know :-)

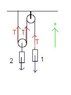
Non-extensible cable attached to ceiling. Cable goes down, around a pulley and then back up, then over another pulley and down. At the end of the cable is mass 1. Hanging from the first pulley is mass 2. I am trying to find a formula for the acceleration of M1 as a function of the mass of 1 and 2.

Homework Equations

I have set g = -9.8m/s^2 (positive acceleration is up, negative is down)

I have a free-body diagram for mass 1:

Total force on mass 1: f1 = f1(up) + f1(down)
f1(up) is the force imparted by the cable pulling up
f1(down) = m1 * g

And for mass 2:

Total force on mass 2: f2 = 2 * f2(up) + f2(down)
f2(up) is the force imparted by each of the two cables lifting on the pulley above mass 2.
f2(down) = m2 * g

I set also f2(up) = f1(up) since the same cable that holds mass 1 also goes to the pulley for mass 2. This is my first question - is this assumption of the forces upward correct?

I also say that because of the pulley arrangement the acceleration of mass 1 (a1) = 2 * the acceleration of mass 2 (a2). I say this because the velocity of mass 1 is double the velocity of mass 2 (due to the pulley arrangement).

So we have:

a1 = 2 * a2
f2(up) = f1(up)
a1 = (f1(up) + f1(down)) / m1
a2 = (2 * f2(up) + f2(down)) / m2

Is this correct so far?

The Attempt at a Solution

Then I try to solve for a1 in terms of m1 and m2.

First, solve for f1(up) in terms of a1:

a2 = (2 * f2(up) + f2(down)) / m2
a2 * m2 = 2 * f2(up) + f2(down)
a2 * m2 = 2 * f1(up) + m2 * g
(a2 * m2) - (m2 * g) = 2 * f1(up)
((a2 * m2) - (m2 * g)) / 2 = f1(up)
(((a1 / 2) * m2) - (m2 * g)) / 2 = f1(up)

Now plug this into the original a1 equation:

a1 = (f1(up) + f1(down)) / m1
a1 = ((((a1 / 2) * m2) - (m2 * g)) / 2 + f1(down)) / m1
a1 = ((((a1 / 2) * m2) - (m2 * g)) / 2 + m1 * g) / m1
a1 * m1 = (((a1 / 2) * m2) - (m2 * g)) / 2 + m1 * g
2 * a1 * m1 = (a1 / 2) * m2 - (m2 * g) + 2 * m1 * g
2 * a1 * m1 - (a1 / 2) * m2 = 2 * m1 * g - (m2 * g)
a1 * (2 * m1 - m2 / 2) = g * (2 * m1 - m2)
a1 = (g * (2 * m1 - m2)) / (2 * m1 - m2 / 2)

Now, as a sanity check, I try some examples:

Example 1:

m1 = 1 kg
m2 = 2 kg
(I would expect this to show no acceleration)

a1 = (-9.8 (2 * 1 - 2)) / (2 * 1 - 2 / 2) = 0
good!

Example 2:

m1 = 1.1 kg
m2 = 2 kg
(I would expect this to show a slow negative acceleration as m1 falls to the floor)

(-9.8 (2 * 1.1 - 2)) / (2 * 1.1 - 2 / 2) = -1.96 / 1.2 = -1.63 m/s^2
good!

Example 3:

m1 = 0.9 kg
m2 = 2 kg
(I would expect this to show a slow positive acceleration as m1 rises to the ceiling)

(-9.8 (2 * 0.9 - 2)) / (2 * 0.9 - 2 / 2) = 1.96 / 0.8 = 2.45 m/s^2
good!

Example 4:

m1 = 0.1 kg
m2 = 2 kg
(I would expect this to show a fast positive acceleration as m1 rises quickly to the ceiling)

(-9.8 (2 * 0.1 - 2)) / (2 * 0.1 - 2 / 2) = 17.64 / -0.8 = -22.05

Huh?

I have been through this several (many!) times and cannot figure out what I'm doing wrong. Can anyone offer some insight?

Additionally, with m1 = 0.5 kg the equation produces zero in the denominator, which is probably not right :-/

Thanks very much in advance!

 

[barryj]

I set up the problem a little differently . I said..

m1g - f(up) = m1a
m2g-2F(up) = m2(a/2)

I solved for a and got

a = 2g(m2-2m1)/(m2-4m1)

for m1 = 1 and m2 = 2 a = 0
for m1 = 1.1 and m2 = 2 a = -1.635
for m1=.9 and m2 = 2 a = 2.45

 

[ehild]

You mixed up the signs. The block 1 and 2 move in opposite directions so a₁=-2a₂.

It is a bit difficult to follow your notations. The upward forces come from the tension in the string, and it is the same everywhere if the pulleys and the string itself are massless. We usually denote the tension by T. Taking upward the positive direction, you have the equations

m₁a₁=T-m₁g
m₂a₂=2T-m₂g
and a₁=-2a₂

ehild

 

[barryj]

I tried to use your notation. F(up) is the same as T.
I am using F = ma for both masses to get the two equations.
For m2, F = m2g - 2T
for m1 F = m1g - T

m1g - T = m1a
m2g-2T = m2(a/2)

solve for T in both equations, T = T can solve for a in terms of m1 and m2.I solved for a and got

a = 2g(m2-2m1)/(m2-4m1)

for m1 = 1 and m2 = 2 a = 0
for m1 = 1.1 and m2 = 2 a = -1.635
for m1=.9 and m2 = 2 a = 2.45
Report

 

[ehild]

I tried to use your notation. F(up) is the same as T.
I am using F = ma for both masses to get the two equations.
For m2, F = m2g - 2T
for m1 F = m1g - T

m1g - T = m1a
m2g-2T = m2(a/2)

If a is the acceleration of m₁, the acceleration of m₂ can not be a/2, as they move in opposite directions (one upward, the other downward).


ehild

 

[johnschmidt]

I set up the problem a little differently . I said..

m1g - f(up) = m1a
m2g-2F(up) = m2(a/2)

I solved for a and got

a = 2g(m2-2m1)/(m2-4m1)

Hi barryj,

You have the same problem I do where for certain values of m1 and m2 you get a zero in the denominator.

 

[johnschmidt]

You mixed up the signs. The block 1 and 2 move in opposite directions so a₁=-2a₂.

It is a bit difficult to follow your notations. The upward forces come from the tension in the string, and it is the same everywhere if the pulleys and the string itself are massless. We usually denote the tension by T. Taking upward the positive direction, you have the equations

m₁a₁=T-m₁g
m₂a₂=2T-m₂g
and a₁=-2a₂

ehild

Yes, you're right! The wrong sign on a was the key.

Now I get:

a1 = 2g(2m1 - m2) / (m1*p^2 + m2)

Plugging in -9.8m/s^2 for g gives:

m1 = 2 kg
m2 = 2 kg
a1 = -3.92 m/s^2

m1 = 1 kg
m2 = 2 kg
a1 = 0 m/s^2

m1 = 0.9 kg
m2 = 2 kg
a1 = 0.7 m/s^2

m1 = 0.5 kg
m2 = 2 kg
a1 = 4.9 m/s^2

m1 = 0.1 kg
m2 = 2 kg
a1 = 14.72 m/s^2

And no more possibility of zero in the denominator (unless both m1 and m2 are zero).

Thanks!

 

[barryj]

Hmmmmm... Good points from both of you.

I'll have to think about this. I assumed I was correct since the sanity checks were sane,