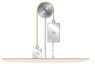Pulley Mass Calculation: Atwood's Machine

  • Thread starter Thread starter becca89
  • Start date Start date
  • Tags Tags
    Mass Pulley
Click For Summary
SUMMARY

The discussion focuses on calculating the mass of a pulley in an Atwood's machine scenario involving two masses (m1 = 5.0 kg and m2 = 3.0 kg) and a uniform disk pulley with a radius of 12 cm. The initial height of m1 is 0.92 m, and its final speed upon hitting the ground is 1.1 m/s. The solution requires applying the conservation of energy principle, specifically the equation K = 1/2mv² + 1/2Iw², where I = 1/2mr². Participants emphasize the importance of including gravitational potential energy in the calculations.

PREREQUISITES
  • Understanding of conservation of energy principles
  • Familiarity with rotational dynamics and moment of inertia
  • Knowledge of kinematic equations
  • Basic algebra for solving equations
NEXT STEPS
  • Review the conservation of energy in mechanical systems
  • Study the moment of inertia for different shapes, particularly disks
  • Learn how to apply kinematic equations in Atwood's machine problems
  • Explore gravitational potential energy calculations in physics
USEFUL FOR

Students studying physics, particularly those focusing on mechanics, as well as educators looking for examples of energy conservation in systems involving pulleys and masses.

becca89
Messages
1
Reaction score
0

Homework Statement



The two masses (m1 = 5.0 kg and m2 = 3.0 kg) in the Atwood's machine shown in Figure 10-23 are released from rest, with m1 at a height of 0.92 m above the floor. When m1 hits the ground its speed is 1.1 m/s. Assume that the pulley is a uniform disk with a radius of 12 cm.

Determine the pulley's mass.


Homework Equations


Conservation of Energy Ef=Ei
K= 1/2mv2+1/2Iw2 (w = omega)
I = 1/2mr2


The Attempt at a Solution



I tried to cancel out as much as I could form the "K" equation and fill it in. Webassign keeps determining my answer wrong...
 

Attachments

  • 10-23.gif
    10-23.gif
    6.5 KB · Views: 633
Physics news on Phys.org
Show what you did. Hint: Don't forget gravitational potential energy.
 

Similar threads

3 pulley problem with attached masses
  • · Replies 15 ·
Replies
15
Views
7K
Using Effective Mass to find the accelerations of 3 masses connected by pulleys
  • · Replies 25 ·
Replies
25
Views
4K
Atwood with Sliding mass and real pulley
  • · Replies 4 ·
Replies
4
Views
4K
Angular acceleration of an atwood pulley
  • · Replies 8 ·
Replies
8
Views
4K
Solve Pulley-Mass System: m1=4.00 kg, m2=1.00 kg
  • · Replies 2 ·
Replies
2
Views
2K
Angular Acceleration and Linear Acceleration of a Pulley
  • · Replies 4 ·
Replies
4
Views
2K
Double pulley Atwood machine (with 3 masses)
  • · Replies 97 ·
4
Replies
97
Views
17K
Acceleration of rising mass and tension in cord
  • · Replies 33 ·
2
Replies
33
Views
3K
What Are the Accelerations and Tensions in a Double Atwood's Machine System?
  • · Replies 8 ·
Replies
8
Views
10K
Acceleration of a block on a massive pulley
  • · Replies 1 ·
Replies
1
Views
2K