Pulley question / rotational kinematics

[alco19357]

Homework Statement

Summary:
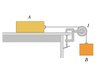
The pulley in the figure has radius (R) and a moment of inertia (I). The rope does not slip over the pulley, and the pulley spins on a frictionless axle. The coefficient of kinetic friction between block A and the tabletop is \mu_k. The system is released from rest, and block B descends. Block A has mass (m_a) and block B has mass (m_b).

Question:
Use energy methods to calculate the speed of block B as a function of the distance (d) that it has descended.
Express your answer in terms of the variables m_a, m_b, R, I, \mu_k, d and appropriate constants

Homework Equations

Conservation of Energy:

PE_i + KE_i = PE_f + KE_f + frictional work

The Attempt at a Solution

(m_agd) + (m_bgd) = m_aV_a²/2 + m_bV_b²/2 + I\omega²/2 + \mu_kmg

0 + (m_bgd) = 0 + m_bV_b²/2 + I\omega²/2 + \mu_kmg


Is this right?

 

[kuruman]

0 + (m_bgd) = 0 + m_bV_b²/2 + I\omega²/2 + \mu_kmg


Is this right?

Two questions
1. Why is this zero?
2. Which mass is this?

 

[alco19357]

1. I don't know. I thought maybe that the velocity of a is non existent, but wouldn't the velocity of a equal the velocity of b?

2. I would say since the frictional work done is between the surface and object a, that mass should be the mass of block a.

Thank you for your help

 

[kuruman]

1. I don't know. I thought maybe that the velocity of a is non existent, but wouldn't the velocity of a equal the velocity of b?

If the velocity of a were zero and the velocity of b were not, the distance between the two blocks would increase in which case the rope connecting them would stretch. This is not what happens. If the rope is not to stretch (or shrink), the two blocks must always have the same instantaneous velocity and acceleration.

2. I would say since the frictional work done is between the surface and object a, that mass should be the mass of block a.

Correct. Now put it together.

 

[alco19357]

Thank you for the help. I applied what you said and got the following answer:

What have I done wrong?

Thanks

 

[kuruman]

Look at your numerator under the radical. You are adding two terms that are dimensionally inconsistent. What are the dimensions of each term?

 

[alco19357]

I think what you're saying is that I have:

[(m^3) / (s^2)] - [(m^2) / (s^2)]

So am I missing the d variable? So should it be:
(m_B * g * d) - (u_k * m_A * g * d)

 

[kuruman]

Yes, that's what the numerator under the radical ought to be.

 

[alco19357]

Thank you so much!

That's the right answer!