Pulley system: 2 pulleys and 3 mass

[alaix]

Homework Statement

Note: My textbook and first language is french, I am sorry if I mistranslated some terms.

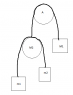
A friction-less rope goes around the fix pulley A. At one side of the rope, there is a mass M1. On the other side, there is a pulley of mass M2. Another friction-less rope goes around that second pulley. Mass m1 and m2 are at the extremeties. Show that the acceleration of mass m1 is given by:

$\frac{3*m2*M2-m1*M1-m1*M2-m2*M1-4*m1*m2}{(m2+m1)*(M1+M2)+4*m1*m2}$

Homework Equations

$\sum F = ma$

The Attempt at a Solution

[URL]http://imgur.com/1OzYU[/URL]

For the first part, where we take The pulley M2 and the mass M1:
M1*a = M1*g-T where T is the tension
-(M2+m1+m2)a = (M2+m1+m2)g - T

T = M1g-M1a

a = $\frac{-(M1-M2-m1-m2)}{M1+M2+m1+m2} g$

Then I take the second part separately:

m2a = m2g -T2 where T2 is the tension in that second rope
-m1a = m1g - T2

T2 = m2g-m2a

a = $\frac{m2-m1}{m2+m1} g$


Then I add both acceleration to have the total acceleration of m1

$a_{total} = (\frac{m2-m1}{m2+m1} - \frac{M1-M2-m1-m2}{M1+M2+m1+m2}) g$

I tried to put both fractions on same denumerator both my answer =/= to the answer I should get...

What am I doing wrong?

 

[gneill]

You start by finding the tension and acceleration for the rope on the fixed pulley, but you're only taking into account masses M1 and M2. Masses m1 and m2 will have some effect, too.

You can take their effect into account by adding 2xT2 to the force that M2 is contributing to the M1/M2 subsystem, or you can start with the M2 subsystem instead, where M2 is assumed to be accelerating with some as yet unknown acceleration a. Note that this 'a' will affect the whole m1/M2/m1 subsystem -- in effect it alters the 'g' that it is working with...