Clara Chung
- 300
- 13
Homework Statement
Homework Equations
The Attempt at a Solution
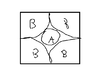
So i got the answer by finding the diagonal of the square and then find the radius of A.
([(2x0.17)2 ]x2 )1/2 = 2a + 2x0.17
And find out a= 0.14 nm , however the answer is 0.124nm, please help