Question about Cyclical Matrices and Coplanarity of Vectors

[kostoglotov]

MIT OCW 18.06 using Intro to Linear Algebra by Strang

So I was working through some stuff about Cyclic Matrices, and the text was talking about how the column vectors that make up this cyclic matrix, shown here,

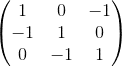
are coplanar, and that is the reason that Ax = b will have either infinite solutions or no solutions depending on what b is; specifically whether or not b₁ + b₂ + b₃ = 0.

I also noticed that the scalar triple product using the three vectors constructed from the columns of the matrix is of course 0, this is to be expected, but if you construct the vectors from the rows of the matrix, the scalar triple product of those vectors is also zero...

Is this just coincidence, or will sets of vectors constructed from both the columns and the rows of a cyclic matrix always be coplanar, or rather, linearly dependent?

 

[Geofleur]

Not all cyclic matrices have coplanar columns or rows and hence vanishing determinants. However, for any matrix $A$, cyclic or not, the following statements are equivalent:

1. det($A$) = 0
2. The columns of A are linearly dependent

Also, because det($A^T$)=det($A$), if the columns of a matrix are linearly dependent, the rows will be too.