Question on a Gauss's Law problem

[dliu1004]

Summary:: I understand the basics of Gauss's Law and how to solve some of the simpler problems, but I cannot seem to solve these two questions.

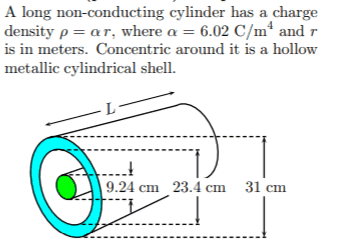
For question 007, one of my friends told me I had to ignore the outer shell? I did that: I integrated rho dV: (6.02*r*pi*r^2*h) from r=0 to r=.0462 and set that equal to epsilon(naught)*E*2pi*0.188*h (this is: epsilon(naught) * the closed integral of E dA) and solved for E. Yet, this was incorrect.

For question 008, I calculated the total enclosed charge per unit height of the inner cylinder per meter by integrating rho dV from r=0 to r=.0462. I got something like q(enc)=0.00002154*h, so that means the charge of the inner surface of the hollow cylinder must be -0.00002154*h, right? I then divided that by the surface area of the inner surface, which was 2*pi*.117*h to get charge per unit area, yet, this was also incorrect.

Thanks in advance!

 

[TSny]

For question 007, one of my friends told me I had to ignore the outer shell? I did that: I integrated rho dV: (6.02*r*pi*r^2*h) from r=0 to r=.0462

So, your integrand for calculating the charge Q on a length $h$ of the inner cylinder is (including the $dr$) $$(6.02 \frac{C}{m^4}) r \pi r^2 h dr$$

Note that overall, this does not have the units of charge since $r \pi r^2 h dr$ has units of $m^5$. I think the problem is with the $\pi r^2$ part of your expression.

What is the volume of a thin cylindrical shell of inner radius $r$, outer radius $r+dr$, and length $h$?