Questioning My Understanding: Is My Answer Wrong?

[NTesla]

Homework Statement

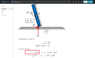
A uniform rod is kept vertically on a horizontal smooth surface at point O. If it is rotated slightly and released, it falls down on the horizontal surface. The lower end will remain:
(a) at O.
(b) at a distance less than $l/2$ from O.
(c) at a distance $l/2$ from O.
(d) at a distance larger than $l/2$ from O.

Relevant Equations

$\tau=I\alpha$

According to me, (a) is the correct answer. However, it's not the right answer according to the book I'm reading.

My understanding is that about point O, there will be a torque due to rod's weight, which will rotate the rod about point O. For eg, if I take a pencil and make it stand vertically on the table, and then rotate it slightly and then release it, it's bottom most point which touches the surface will not move, the whole pencil will rotate about the point O due to torque due to its weight. As such, the lower end will remain at point O.

But my answer is wrong according to the book.
Can someone please tell why my answer is wrong ?

 

[Steve4Physics]

Can you name all the forces (plus their points of application and directions) acting:
a) on your pencil when toppling over on your table;
b) on the rod when toppling over on the smooth (frictionless) surface?

 

[NTesla]

Same diagram will be applicable for both, the pencil and the rod. I took the example of pencil as it can also be construed as a uniform rod.

 

[kuruman]

Yes, the diagrams may be the same, but what about the forces? Suppose the tip stays at point O as you say. When the rod/pencil is at an angle and rotating about O, what force is needed to keep the center of mass going in a circle? What agent outside the rod/pencil system can exert such a force?

 

[NTesla]

@kuruman,

 

[Steve4Physics]

Same diagram will be applicable for both, the pencil and the rod. I took the example of pencil as it can also be construed as a uniform rod.

The forces are different. Three forces on the pencil. Two forces on the rod.

Hint: Once you've sussed-out the forces, you can work out what happens to the rod's centre of mass and the problem becomes trivial.

 

[haruspex]

@kuruman,
View attachment 274077

It's more useful to think about forces and accelerations in the horizontal direction, rather than rotation.

 

[NTesla]

The forces are different. Three forces on the pencil. Two forces on the rod.

Hint: Once you've sussed-out the forces, you can work out what happens to the rod's centre of mass and the problem becomes trivial.

@Steve4Physics, 3 Forces on the pencil !
One is definitely weight due to gravity, another is Normal reaction from surface, I don't know what the 3rd one is. And I've assumed a pencil to be as a uniform rod, then how come, there would be only 2 forces on the rod but 3 on the pencil ?

 

[Steve4Physics]

@Steve4Physics, 3 Forces on the pencil !
One is definitely weight due to gravity, another is Normal reaction from surface, I don't know what the 3rd one is. And I've assumed a pencil to be as a uniform rod, then how come, there would be only 2 forces on the rod but 3 on the pencil ?

Your pencil has friction at O. Assuming the limiting frictional force is large enough, the pencil's base won't slide. But you are told the rod is on a "smooth" (= frictionless) surface.

 

[NTesla]

Your pencil has friction at O. Assuming the limiting frictional force is large enough, the pencil's base won't slide. But you are told the rod is on a "smooth" (= frictionless) surface.

I was assuming the pencil to be standing on the smooth surface as well, hence the two forces.
However, in post#5, as a component of Normal force provides the required centripetal force, why wouldn't the CoM move in a circular trajectory ?

 

[kuruman]

I agree that to get the CoM to move in a circular trajectory, you will a centripetal force component. Where would that component come from? If there no friction, the table can only exert a force straight up, perpendicular to the surface and gravity is antiparallel to it straight down. Neither has a horizontal component. In post #5 there should be no friction and therefore no N cosθ.

 

[NTesla]

In post #5 there should be no friction and therefore no N cosθ.

@kuruman, I understand that there is no friction, but why have you written no friciton therefore no N$Cos\theta$. What is wrong in taking a component of a force at an angle to the line of action of the force. Isn't it just separating the components in a particular direction ?

 

[haruspex]

I was assuming the pencil to be standing on the smooth surface as well, hence the two forces.
However, in post#5, as a component of Normal force provides the required centripetal force, why wouldn't the CoM move in a circular trajectory ?

@kuruman, I understand that there is no friction, but why have you written no friciton therefore no N$Cos\theta$. What is wrong in taking a component of a force at an angle to the line of action of the force. Isn't it just separating the components in a particular direction ?

As I hinted in post #7, the simplest approach here is to think about the net horizontal force and consequent horizontal acceleration of the mass centre.

 

[kuruman]

@kuruman, I understand that there is no friction, but why have you written no friciton therefore no N$Cos\theta$. What is wrong in taking a component of a force at an angle to the line of action of the force. Isn't it just separating the components in a particular direction ?

A vertical force has no horizontal component by definition. Both forces in this example are vertical.

 

[NTesla]

A vertical force has no horizontal component by definition. Both forces in this example are vertical.

@kuruman, Yes a vertical force has no component in horizontal direction, but at an angle $\theta$ can't it have a component ?
Like when a particle is sliding down a wedge, component of it's weight along the surface of the wedge is mgsin$\theta$, and it's component perpendicular to the surface of the wedge is mgCos$\theta$. What's wrong in taking the same approach in the present case ?

 

[haruspex]

as a component of Normal force provides the required centripetal force

No, it would point radially up, not radially down.
And you cannot be sure there is a centripetal force here.

 

[NTesla]

No, it would point radially up, not radially down.
And you cannot be sure there is a centripetal force here.

@haruspex, Yes N is upward i.e. Normal to the surface. Even then, why can we not say that NCos$\theta$ is providing the centrifugal force given by NCos$\theta$=$mw^2r$ ?

 

[haruspex]

@haruspex, Yes N is upward i.e. Normal to the surface. Even then, why can we not say that NCos$\theta$ is providing the centrifugal force given by NCos$\theta$=$mw^2r$ ?

You previously said centripetal force, so first we need to clear up what these two things are.

Centrifugal force is an apparent force that results from using a noninertial frame. It is not an actual force, so is not provided by any combination of applied forces. If spun in a drum, you notice a normal force from the wall, but, in your frame of reference, you are not accelerating, so to explain the unbalanced normal force your brain invents a force pushing you against the wall.

Centripetal force is real, but it is not a specific applied force or sum of such: it is that component of the sum of applied forces which acts orthogonally to the velocity.

In the present situation, you cannot assume that the sum of applied forces has a component orthogonal to the velocity of the mass centre, so you cannot assume there is a centripetal force.

If you suppose the rod is rotating about an axis below its mass centre then the centripetal force must be acting at some downward angle. The normal force from the ground clearly does not do that. Indeed, if we say instead that there is friction to hold the base of the rod in place then it is the gravitational force force that supplies the downward component of the centripetal force.

But, please, can we set aside all this discussion of centrifugal/ centripetal forces until we have solved the question at hand by the very simple approach of applying F=ma to the horizontal aspects?

 

[Steve4Physics]

@haruspex, Yes N is upward i.e. Normal to the surface. Even then, why can we not say that NCos$\theta$ is providing the centrifugal force given by NCos$\theta$=$mw^2r$ ?

As haruspex explains, you mean 'centripetal'. However, forget about the rotation until you can answer these 2 simple questions:
Q1. What is the direction of the resultant force on the rod while it topples?
Q2. Therefore what happens to the rod's centre of mass while it topples?

 

[NTesla]

As haruspex explains, you mean 'centripetal'. However, forget about the rotation until you can answer these 2 simple questions:
Q1. What is the direction of the resultant force on the rod while it topples?
Q2. Therefore what happens to the rod's centre of mass while it topples?

@Steve4Physics, the resultant of net force is downward, hence the CoM goes down, but mg creates a torque about the point at which the rod touches the surface.

 

[NTesla]

until we have solved the question at hand by the very simple approach of applying F=ma to the horizontal aspects?

@haruspex, If we use F=ma, then since there is no force/neither a component of any force in the horizontal direction, therefore the CoM must not move in the horizontal direction. I get that. But why is it difficult to explain /understand from rotation point of view.
If we take the FoR of the rod itself, then it is a non-inertial FoR. Therefore it could be said that NCos$\theta$ is providing the centrifugal force, and therefore the CoM must move in circular trajectory, i.e. the rod will rotate about point O.

 

[Steve4Physics]

@Steve4Physics, the resultant of net force is downward, hence the CoM goes down, but mg creates a torque about the point at which the rod touches the surface.

Yes, the resultant force is vertically downwards, so the CoM accelerates vertically downwards. Can you answer the original question now?

Understanding the rotation is much much complicated. The rod has both a resultant force and a couple acting on it; neither of these is constant which makes analysing the rotation tricky. Considering rotation about the centre of mass, the couple is entirely due to the normal reaction . However both the magnitude and lever-arm of the normal reaction change over time. But to answer the original question, this is irrelevant.

 

[NTesla]

Yes, the resultant force is vertically downwards, so the CoM accelerates vertically downwards. Can you answer the original question now?

Understanding the rotation is much much complicated. The rod has both a resultant force and a couple acting on it; neither of these is constant which makes analysing the rotation tricky. Considering rotation about the centre of mass, the couple is entirely due to the normal reaction . However both the magnitude and lever-arm of the normal reaction change over time. But to answer the original question, this is irrelevant.

@Steve4Physics, I can answer it like this: Since no component of force in horizontal direction, therefore no movement of CoM in horizontal direction.

But I wish to understand it in totality, not just in one way, as in no horizontal force, therefore no horizontal acceleration, therefore no horizontal movement. I also need to understand it in terms of rotation.

If we are in FoR of rod itself, then will NCos$\theta$ not provide the centrifugal force of $mw^2r$ ? Why won't it.?

 

[Steve4Physics]

@Steve4Physics, I can answer it like this: Since no component of force in horizontal direction, therefore no movement of CoM in horizontal direction.

But I wish to understand it in totality, not just in one way, as in no horizontal force, therefore no horizontal acceleration, therefore no horizontal movement. I also need to understand it in terms of rotation.

If we are in FoR of rod itself, then will NCos$\theta$ not provide the centrifugal force of $mw^2r$ ? Why won't it.?

You first need to to read haruspex's post #18 to understand why it is a serious mistake to use the term 'centrifugal force' here.

Yes, at any instant Ncosθ is the centripetal force. But note N is not constant which complicates the maths. If you want to investigate the maths more deeply, do a search for 'rod falling on frictionless surface'.

For example I found this: https://physics.stackexchange.com/q...od-with-one-end-touching-a-frictionless-surfa (However I don't guarantee the content of the link and the presence of friction seems to have got muddled into the answer.)

 

[jbriggs444]

@Steve4Physics, the resultant of net force is downward, hence the CoM goes down, but mg creates a torque about the point at which the rod touches the surface.

Yes. There is a torque associated with the force of gravity. There being no other forces on the rod that have associated torques, that means that this torque is, at least initially, equal to the net torque on the rod.

That means that the angular momentum of the rod will be changing over time.

What it does not mean is that the rod will be moving horizontally. There is a way that the rod can change angular momentum without moving horizontally -- it can rotate about its center of mass.

Since horizontal motion of the center of mass is ruled out by other arguments, we can be sure that this rotation is at least part of what actually happens.

Note that vertical motion motion of the center of mass also adds to angular momentum about the initial contact point since the center of mass is not on a vertical line with that contact point. Angular momentum is not just about rotation.

 

[Steve4Physics]

Yes. Note that if considering rotation about the CoM, weight passes through this point so produces zero torque about the CoM. The torque about the CoM is produced by the (changing) normal reaction.

 

[jbriggs444]

Yes. Note that if considering rotation about the CoM, weight passes through this point so produces zero torque about the CoM. The torque about the CoM is produced by the (changing) normal reaction.

Yes. What I had in mind was an accounting where we are taking angular momentum about the initial point of contact. We are considering that angular momentum of the rod as being comprised of the rod's angular momentum about its own center of mass plus the angular momentum based on the linear motion of the center of mass about the initial point of contact.

 

[kuruman]

Yes. There is a torque associated with the force of gravity. There being no other forces on the rod that have associated torques, that means that this torque is, at least initially, equal to the net torque on the rod.

That means that the angular momentum of the rod will be changing over time.

What it does not mean is that the rod will be moving horizontally. There is a way that the rod can change angular momentum without moving horizontally -- it can rotate about its center of mass.

Since horizontal motion of the center of mass is ruled out by other arguments, we can be sure that this rotation is what actually happens.

To which I would add that if the rod rotates about the CM, the end touching the floor has to lift off it by an infinitesimally small amount $\delta y$ in which case the normal force goes to zero. When that happens, the CM will fall by another $\delta y$ while rotating some more and so on. In the limit $\delta y \rightarrow 0$ the rod rotates as the CM falls straight down while the normal force is zero.

 

[jbriggs444]

To which I would add that if the rod rotates about the CM, the end touching the floor has to lift off it by an infinitesimally small amount $\delta y$ in which case the normal force goes to zero. When that happens, the CM will fall by another $\delta y$ while rotating some more and so on. In the limit $\delta y \rightarrow 0$ the rod rotates as the CM fall straight down while the normal force is zero.

The normal force is non-zero throughout the event until impact.

One can see this by adopting the point of view taken by @Steve4Physics. The rotation of the rod about its center of mass can only result from the normal force. The rotation is accelerating. So the normal force must be non-zero.

[I have not 100% convinced myself that the rod will not lift free of the surface prior to impact. But it does not seem like it should]

 

[kuruman]

The normal force is non-zero throughout the event until impact.

One can see this by adopting the point of view taken by @Steve4Physics. The rotation of the rod about its center of mass can only result from the normal force. The rotation is accelerating. So the normal force must be non-zero.

OK, I see it now. I got mixed up a bit.

 

[haruspex]

it could be said that NCosθ is providing the centrifugal force

As I posted, nothing "provides" a centrifugal force. It is a consequence of the rotation, not a cause of it.
Not only is the rod accelerating linearly, it is rotating, and the rotation is accelerating.
In the frame of reference of the rod, none of those things are happening, yet it only feels the normal force from the ground. To explain this unbalanced force, we need to bring in two fictitious forces: gravity and the Euler force (a fictitious torque). The combination of these balances the perceived normal force. See
https://en.m.wikipedia.org/wiki/Euler_force.
There is no centrifugal force because the linear acceleration and velocity are collinear.

at any instant Ncosθ is the centripetal force.

No. As I explained, there is no centripetal force here. The mass centre of the rod is accelerating in the direction of its velocity.

 

[NTesla]

As I posted, nothing "provides" a centrifugal force. It is a consequence of the rotation, not a cause of it.
Not only is the rod accelerating linearly, it is rotating, and the rotation is accelerating.
In the frame of reference of the rod, none of those things are happening, yet it only feels the normal force from the ground. To explain this unbalanced force, we need to bring in two fictitious forces: gravity and the Euler force (a fictitious torque). The combination of these balances the perceived normal force. See
https://en.m.wikipedia.org/wiki/Euler_force.
There is no centrifugal force because the linear acceleration and velocity are collinear.

No. As I explained, there is no centripetal force here. The mass centre of the rod is accelerating in the direction of its velocity.

@haruspex, In the non-inertial FoR, centrifugal force IS the cause. How could it ever be an effect. For eg.: If an ant begins his life inside a rotating cylinder, will he not experience centrifugal force as a cause by which it is sticking on the inside surface of the cylinder.

In the article in the link provided by @Steve4Physics in post#24: https://physics.stackexchange.com/q...od-with-one-end-touching-a-frictionless-surfa
can somebody please explain how the equation (marked in red rectangle) has been arrived at in the attached file below.

 

[kuruman]

can somebody please explain how the equation (marked in red rectangle) has been arrived at in the attached file below.

It's quite simple. It says that the forward velocity of the center of mass (point C on the rod) relative to the ground is equal to the forward velocity of the point of ground contact A minus the linear velocity of point C as it rotates counterclockwise relative to point A.

Note that this is a different physical situation from what we have here where there is no external force $F$ applied at point A. Therefore, here $\ddot x_C=0$. To repeat what has already been said, if the horizontal acceleration is zero and the rod is initially at rest, point C will not move horizontally. In terms of the constraint equation in the red rectangle this means that $$\dot x_C=0~\Rightarrow~\dot x_A=\frac{l}{2}\dot \theta\cos\theta.$$

 

[haruspex]

In the non-inertial FoR, centrifugal force IS the cause

Is the cause of what, in the context of the falling rod?
I wrote that it is not a cause of the rotation. In your ant example, it is the cause of the ant being forced against the wall, not a cause of rotation of anything.

 

[NTesla]

Is the cause of what, in the context of the falling rod?
I wrote that it is not a cause of the rotation. In your ant example, it is the cause of the ant being forced against the wall, not a cause of rotation of anything.

My understanding is that: In an inertial frame, centripetal force is the cause of rotation, and when viewed from a non-inertial frame of reference, centrifugal force is the cause of rotation.

 

[kuruman]

My understanding is that: In an inertial frame, centripetal force is the cause of rotation, and when viewed from a non-inertial frame of reference, centrifugal force is the cause of rotation.

I agree with the first half of this statement but not the second. Say I am in an inertial frame looking at you standing on a rotating platform at some distance from the rotation axis. I see you rotate and conclude that the force of static friction provides the centripetal acceleration needed to keep you going in a circle. As far as you are concerned, you are not rotating but you experience a centrifugal force which is canceled by the force of friction at your feet, so that you remain at rest in the non-inertial frame. As far as you are concerned, you are not accelerating and the centrifugal force you experience is not the cause of any rotation in your frame.

 

[haruspex]

In an inertial frame, centripetal force is the cause of rotation,

Yes.

when viewed from a non-inertial frame of reference, centrifugal force is the cause of rotation.

No, mostly, but see the example at the end below.

Presumably you mean specifically the frame of reference of the rotating object. In that frame there is no rotation, or motion of any sort, by definition, but there may be unbalanced forces which ought to be causing an acceleration according to Newton's laws. To fix this up, we invent centrifugal force, etc., to represent the rotation of the frame relative to an inertial frame. These fictitious forces are added to the real applied forces.
True, you could take any non-inertial frame, independently of the object, but then things get more complicated. We may observe that the object does rotate about some axis in that frame, but not in a way that seems to match the applied forces.
In this case, we have both centrifugal and centripetal forces:
- centrifugal force (and Coriolis, and Euler, as appropriate), computed from the acceleration of our chosen non-inertial frame, is added to the real applied forces, and,
- of the resultant, the component normal to the observed velocity produces the centripetal force, resulting in the observed centripetal acceleration.

In the case where the observer is being whirled around an axis on the end of a cable, the centrifugal force in the observer's frame points away from the axis and balances the tension in the cable. This results in the zero acceleration the observer records.
In an inertial frame, the tension provides the centripetal force, which points towards the axis.
But now consider Bob, rotating on the spot, observing Alice, standing still nearby (on a frictionless surface, say). To Bob, Alice appears to be rotating around him, so accelerating towards him, yet not subject to any horizontal forces. In this case, the "centrifugal" force on Alice in Bob's reference frame, when we do the cross product calculation, turns out be pointing towards Bob, and is providing the centripetal acceleration Bob perceives.

 

[Richard R Richard]

Let's do some formulas
The problem says that a small imbalance is used to cause the rod to overturn, we can assume that the initial angular and linear momentum wasn't significantly altered.
As already said, if there is no friction, the ground cannot push the rod by horizontal reaction force, because there is no horizontal component of weigth, then there is no change in the linear moment of the center of mass, therefore its horizontal position remains constant, response b. End of problem, but we can calculate 3 results from different situations .
An energy analysis shows
$$ \dfrac {L} {2} mg = \dfrac12mv_{CM} ^ 2 + \dfrac12I_{CM} \omega_{CM} ^ 2 $$
An instant before hitting the floor it is verified that if N> 0 during the entire fall then
$$ \omega_{CM} = \dfrac {v_{CM}} {\frac L2} $$
Since $I_{CM} = \dfrac {1} {12} mL ^ 2$
Resulting that $$ v_{CMx} = 0 $$ and that $$ v_{CMy} = \sqrt {\dfrac {3Lg} {4}} $$
If $\mu_s$ is large enough that the fulcrum does not move then the energy balance system becomes
$$ \dfrac {L} {2} mg = \dfrac12mv_{CM} ^ 2 + \dfrac12I_{ext} \omega_{CM} ^ 2 $$
As now the instantaneous center of rotation changes to the lower end of the rod
Since $I_{ext} = \dfrac {1} {3} mL ^ 2$
Then $$ v_{CMx} = 0 $$ and that $$ v_{CMy} = \sqrt {\dfrac {3Lg} {7}} $$ the position of the CM on impact is $L /2$ away from position $x_o$
But always at some point, , if the rod is free for move
$$ mg \sin \theta> \mu mg \cos \theta \quad \to \quad \mu <\tan \theta $$
and at that moment the support point slides losing kinetic energy, the calculation of the final position of the CM becomes complex depending on the value of the work of the friction force which is a variable force in time and the length it slides as well.

 

[haruspex]

if N> 0 during the entire fall

Is there a trivial way to prove that?
It always bothers me with questions about falling and rotating rods that the question setter seems to overlook the possibility that the rod becomes airborne. I believe there is no such in the present case, but it can occur in other scenarios, such as a rod that had been standing against a wall.

 

[Richard R Richard]

Is there a trivial way to prove that?

Is there a time during fall when the modulus of the angular velocity of rotation multiplied by the radius is greater than the rate of fall of the center of mass? In this case no, in fact the angular acceleration is the result of a bond between the rod and the ground.

 

[haruspex]

Is there a time during fall when the modulus of the angular velocity of rotation multiplied by the radius is greater than the rate of fall of the center of mass?

When the rod length 2r makes angle theta to the vertical, if the base is remaining in contact with the ground then the vertical velocity of the mass centre is $v=\omega r\sin(\theta)$, so for θ <π/2 yes, $r\omega>v$.
At first, most of the KE will be in the rotation. The concern then is whether the angular momentum may become so great that the downward velocity can't catch up.