- #1
Bigworldjust
- 54
- 0
Homework Statement
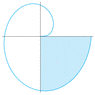
Find the area of the shaded region.
r=sqrt(θ)
Homework Equations
A = integral from a to b 1/2r^2dθ
The Attempt at a Solution
I know how to solve the question, I just don't know what to use for a and b. I tried 0 and 2pi but I am getting the wrong answer. Here is a picture:
http://www.webassign.net/mapleplots/a/8/0c017c152b2f6bb8c6df656e3a1bc2.gif
Thank you for the help. I just need to know what parameters to use for a and b :).