Ramp on unknown unlevel surface

[zacharoni16]

I'm hoping someone here could help me with a problem I am having. I have an electronic sensor that measures tilt, and I put this sensor on a 10 degree ramp. The problem is that this portable ramp is put on surfaces that the levelness is unknown. It can vary up to +/- six degrees. The bottom of the ramps are perfectly flat, and the ramp angle is always 10 degrees accurate to 15 arc-seconds.

Here is the procedure I use, first I put the sensor on the surface to take an angle measurement. I store this measurement, then the user places the ramp on the surface, and the sensor on the 10 degree ramp surface.

The Problem

The user can place the ramp any direction on the surface, and the surface and be "unlevel" any direction such as -5 degrees or +2 degrees, etc.

Here is a quick mspaint picture (The triangle 10 degrees are not to scale, they look more like 45 degrees (sorry)):

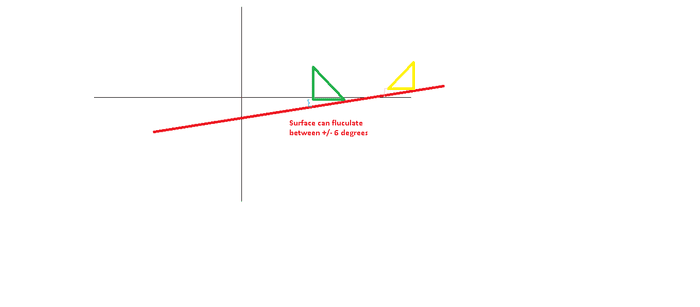
The two main situations I'm most concerned about are:

Case 1:

The green ramp is placed so that the "high" portion of the ramp is set on a surface sloping low to high. So the surfaces low angle subtracts from what the sensor will read on the 10 degree ramp (Blue curly bracket under ramp)

Case 2:

The yellow ramp is placed so that the "high portion of the ramp is set on the surface sloping high to low so the surface adds to the angle measured by the sensor on the 10 degree ramp surface. (orange curly bracket under ramp)


I want to mathematically "zero" this surface out so it has no effect on the 10 degree ramp measurement by the sensor. Right now I'm just measuring the surface angle and subtracting it from the measurement of the 10 degree ramp for a relative angle. Plus this gets messed up if I need to add the surface angle or subtract it. Am I right in this line of thought?

I wanted to know if there is a better way to do this so if the user places the ramp in any direction of the surface I can zero it out so the sensor could read the 10 degree ramp without having the surface affect the measurement.

Thinking there might be a trig solution..

The sensor is a single axis sensor, so it should be easier I would think

Thank you

 

[mfb]

With a single sensor, you cannot measure the angle of the ramp - the yellow and green case are the extreme examples, and the sensor cannot measure rotation and slope at the same time. A 2D sensor with a known orientation would work, alternatively record the maximal and minimal tilt or something similar. Or find a way to fix the ramp orientation relative to the surface.

 

[zacharoni16]

With the single sensor I first measure the surface, then I measure the ramp. So when the sensor is on the ramp I already measured the surface angle. I'm thinking I could just add or subtract the angle measured when the sensor was on the surface? This would negate the surface's affect on the ramp reading of the sensor at least I would think?

My problem right now is that I'm trying to combine these voltage measurements into a single equation for an angle:

tilt sensor that acts sort of like a potentiometer. It is an electrolytic sensor that acts sort of like a balance. One side increases in voltage while one side lowers voltage. The sum of both voltages must add up to 4VAC.

the sensor has a nominal scale factor of 0.174mV/degree

When I put the sensor on a surface I take two voltage measurements

One side angle = (SideAvoltage - 2.00) / 0.174

Other side = (2.00 - SideBvoltage) / 0.174

I'm looking for a way to combine these into one equation so I can calculate magnitude and direction of the angle.

Would it be sort of a vector sum?

One side voltage is increasing and one side is decreasing

 

[mfb]

If you do not know the orientation on the ramp, you have three degrees of freedom:
- the angle of the surface (determined with the first measurement)
- the angle of the slope
- the relative orientation between ramp and surface tilt

You need at least three measurements to solve this problem, you just have two.

I'm thinking I could just add or subtract the angle measured when the sensor was on the surface?

If you are sure the ramp is in the green or the yellow position, yes. If your surface can tilt by several degrees and you want an arcsecond precision, this is not trivial.

When I put the sensor on a surface I take two voltage measurements

The relation between voltage measurements and tilt is a separated problem. The calibration of the device should give this.

 

[zacharoni16]

For now the user is constrained to place the ramp in the yellow and green positions to make the problem simpler

 

[mfb]

Then I don't see the problem. Just subtract or add, depending on the position the user picks.
If you do not know this, you get the same issue again. If the surface is tilted sufficiently, one value might be so far away that you can discard it.