tracyellen said:
I am sorry. I don't really know how to find a PE of an item without any numbers. I am used to a length or something to help me out. That is why I am having such a hard time with this problem. :(
tracyellen said:
Maybe E=KEo...but again I don't know how to make that work with this problem. I am not really looking for an answer for I have already turned in the wrong one. I am just trying to figure out how I got it wrong and how to do it right. :)
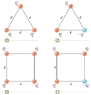
I think it's helpful to show the figure full size.
Start with no charge -- empty space.
It takes zero work to bring the first positive charge into position (for all four configurations).
For A & C, bring a second positive charge into position into position a distance, d, from the first charge. The potential energy stored in such a system is equal to the amount of work required to bring the second charge into position. Call this amount of energy, E
0 .
For A: Bringing a third positive requires twice the work, i.e. 2E
0. Total PE is 3E
0.
For C: Bringing a third positive charge requires a little less work than for A. E
0 to overcome the repulsion of the closer charge. A bit less to overcome the repulsion of the other charge. But then there is a fourth charge!
It takes 2E0 to overcome the repulsion of the two closest charges. A bit less to overcome the repulsion of the other charge.
The total for C: (4 + _)E
0 .
For B & D, bring a second charge, this time a negative charge, into position into position a distance, d, from the first charge. The work needed to do this is -E
0, so that's the potential energy stored in such a system.
For B: Bringing a third charge, this one positive, into its position requires zero work. E
0 to overcome the repulsion of the 1st positive charge & -E
0 due to the attraction of the negative charge.
Total PE for B: -E0 .
D is a little more involved.
Bringing a third charge, this the other positive one a distance, d, from the negative charge, requires -E
0 due to the attraction of the negative charge plus some positive work, a bit less than E
0 overcome the repulsion of the 1st positive charge, because the separation is greater than d. Bringing the forth charge to its position requires 2E
0 to overcome the repulsion of the other two positive charges plus some negative work due to the attraction of the negative charge. This negative PE is a bit smaller in magnitude than E
0 and in fact cancels the the previous positive PE which was a bit less than E
0.
Total PE for D: 0 .