joker2014
- 21
- 0
It statics, I am having difficulty on getting perfect to read the dimensions correctly in order to find the forces!
This photo for example
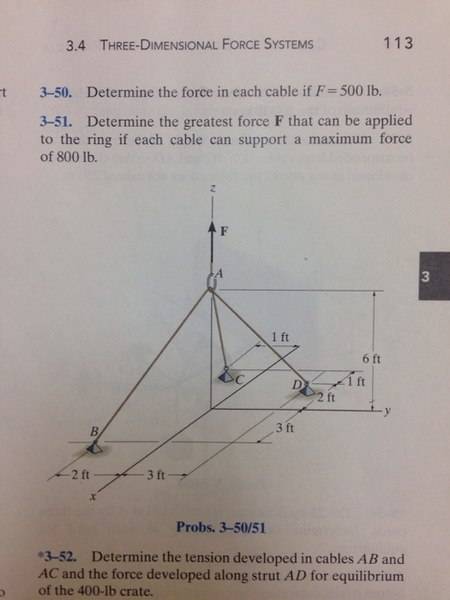
I put B = (-3i,-2j, -6k) but correct answer is (3i,-2j,-6k) ... why 3i but not 3i ?! I'm reeally confused
For C I put -1i but correct answer is 3i !.. how?!?
for D I added the 1 and 2 and i put -3i , and I put -3j but correct is 3j ...
can anyone explain and give me easier way to approach the answer and avoid mistakes?! I have an exam on friday and this is basic thing that i can't seem to understand!
This photo for example
I put B = (-3i,-2j, -6k) but correct answer is (3i,-2j,-6k) ... why 3i but not 3i ?! I'm reeally confused
For C I put -1i but correct answer is 3i !.. how?!?
for D I added the 1 and 2 and i put -3i , and I put -3j but correct is 3j ...
can anyone explain and give me easier way to approach the answer and avoid mistakes?! I have an exam on friday and this is basic thing that i can't seem to understand!