PatsyTy
- 30
- 1
Homework Statement
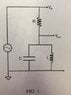
Given the circuit below (image uploaded) driven at a frequency ##ω=2πƒ## show that
$$|\frac{v_{out}}{v_{in}}|=\frac{1}{\sqrt{1+(\frac{1}{ωτ_{l}}-ωτ_{c})^2}}$$
where ##τ_{c}=RC## and ##τ_{l}+L/R##
Homework Equations
##Z_R=R##, ##Z_L=jωL## and ##Z_C=-j/ωC## where ##j=\sqrt-1##
The Attempt at a Solution
I start with
$$\frac{v_{out}}{v_{in}}=\frac{Z_R}{Z_C Z_L / (Z_C+Z_L)+Z_R}=\frac{Z_R(Z_C+Z_L)}{Z_C Z_L+Z_R(Z_C+Z_L)}$$
where the impedance of the resistor, inductor and capacitor are ##Z_R##, ##Z_L## and ##Z_C## respectively. I sub in values for the impedances seeing as I don't think there is any more simplification I can do here
$$\frac{v_{out}}{v_{in}}=\frac{R(-j/ωC+jωL)}{-j/ωC jωL+R(-j/ωC+jωL)}$$
I know I have to get this into a form where I can take the real part of $$\frac{v_{out}}{v_{in}}$$, in other words I want this in the form
$$\frac{v_{in}}{v_{out}}=\frac{A+jB}{C+jD}$$
however I have no idea how to do this, I'm not sure if I have set up the problem wrong. I've tried multiplying through by ##\frac{j}{j}## and ##\frac{-j}{-j}## but it doesn't seem to get me anywhere. I feel I know how to solve most of this problem, I am just unsure how to rearrange this expression to get a usable result.