sakkid95
- 6
- 0
Question link: http://gyazo.com/4d52ab2521e5b222241718ea1b7ccb08.png
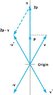
I have to solve this using vectors, not geometry
My professor said the equation that's required is -v* = 2 proj v onto n - v
and v* is reflected vector, so I don't really understand how to do this
First off I don't understand how to use the equation itself, our teacher hasn't done any examples, he just showed us how he derived the equation
My attempt
I found proj of v onto n for the first line was (0, x+a) x is first x value for mirror but I'm not really sure how I'm supposed to subtract the vector, and then I also don't understand how we're supposed to find cotangent in our solution.
If anyone could help explain what I'm supposed to do, I'd be very grateful, thanks.
I have to solve this using vectors, not geometry
My professor said the equation that's required is -v* = 2 proj v onto n - v
and v* is reflected vector, so I don't really understand how to do this
First off I don't understand how to use the equation itself, our teacher hasn't done any examples, he just showed us how he derived the equation
My attempt
I found proj of v onto n for the first line was (0, x+a) x is first x value for mirror but I'm not really sure how I'm supposed to subtract the vector, and then I also don't understand how we're supposed to find cotangent in our solution.
If anyone could help explain what I'm supposed to do, I'd be very grateful, thanks.