Relating Coefficient of Friction for my Tyre Experiment

[Matt.D]

Hi all!

How do you calculate the coefficient of friction for a tyre sample going against concrete?

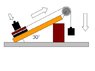
My experiment involves a uniform piece of concrete angled at 30 degrees with a pulley attached at the raised end.
The tyre sample is placed at the end of the concrete slab and is loaded with 1.0kg of weight to keep it in constant contact with the surface.
The tyre sample is connected to a piece of string that runs over the pulley and at is connected at the other end to a 'weight holder', which I continue to add weights to until the rubber sample moves or loses grip.

I've found that the rubber will take 1.3kg of weight before it slips, but how do I translate that to a coefficient of friction?

I've been looking at a number of formulas, but I can't find any that take into account the angle of the surface - 30 degrees, which I'm sure has a direct effect on the experiment.
Also, do I need to take into account the 'load' I've placed on top of the rubber to keep it pressed down, or will this cancel itself out?

I've uploaded a diagram I drew of how the experiment is setup. Please note the downward arrow above the tyre sample is to exagerate the load pressing down onto the surface. The other arrows pointing to the right and downward, next to the pulley, show the direction of force.

Grey = the floor the experiment is taking place
Orange = the concrete (its a garden edging strip, hence the color ; )
Brown = Wood. I've used a wooden block to hold the concrete block in place and a small piece of wood to make a 'mounting block' for the rubber and weight to go on.

Thanks for looking!

Matt

 

[Doc Al]

What your experiment allows you to find is the maximum static friction that the surfaces can support, which relates to the coefficient of static friction by $\mu N = m_2 g$, where N is the normal force pressing the surfaces together and $m_2$ is the mass of the hanging weight. To find the normal force, consider the forces acting on your 1.0 kg mass. (What's the component of its weight normal to the surface?)

 

[what]

It might help you if you drew a freebody diagram for yourself. First label an axis whose origin is at the center of mass and draw the forces acting on the object. You should notice the relation if you know Newtons laws and trig.

 

[Chi Meson]

If you do the math correctly you get one of the most "elegant" formulas in physics as a result (lots of things cancel leaving a very simple relationship).

 

[Doc Al]

Chi Meson makes an important point. Never rush to just "plug in numbers"; always try to work out the physics symbolically as much as possible. Two big benefits of doing this: (1) Things often simplify greatly, thus reducing your source for arithmetic mistakes when you do finally plug in the numbers, and (2) you stand a much better chance of understanding the physics involved instead of getting lost in arithmetic.