Relationship between E-field and Probability Amplitude of Waves

[tade]

Electromagnetic waves can be classically described by Maxwell's equations.

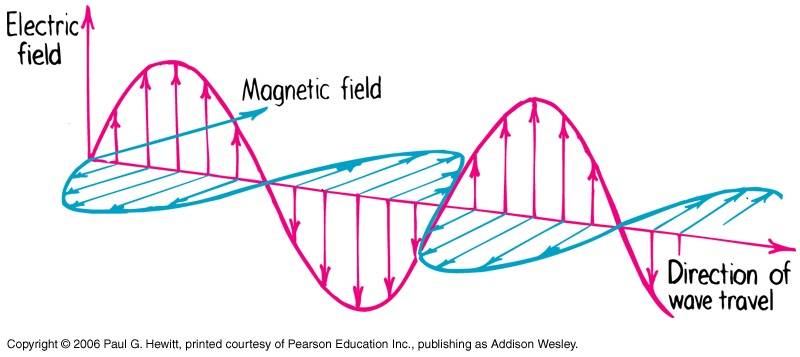
Photons can be described by probability waves.In this case, what is the relationship between the electric field and the probability amplitude?

Are they directly proportional to each other? What about the fact that one is a vector and the other a scalar?

 

[tade]

The Intensity is proportional to the square of the E-field amplitude, and also proportional to the square of the probability amplitude.

 

[tade]

I thought this would be a commonly asked question.

 

[Jilang]

It seems to be quite commonly asked.
https://www.physicsforums.com/threa...een-em-waves-and-photon-wavefunctions.855874/

 

[tade]

It seems to be quite commonly asked.
https://www.physicsforums.com/threa...een-em-waves-and-photon-wavefunctions.855874/

Do you know the answer?

 

[Jilang]

Did you read the thread? Your question stated that photons could be described by probability waves and then asked a question that if that were were the case... The lack of responses would suggest that it cannot be the case.

 

[tade]

Did you read the thread? Your question stated that photons could be described by probability waves and then asked a question that if that were were the case... The lack of responses would suggest that it cannot be the case.

Yeah I know, but I was asking if you yourself know the answer.

 

[blue_leaf77]

A photon is not a non-relativistic object, this implies that its quantum behavior cannot be described by the (non-relativistic) Schroedinger equation. For non-relativistic particles, you can find its position representation wavefunction by solving the Schroedinger equation. Since you can't do that with photon, there is no spatial wavefunction in the usual sense of non-relativistic QM which can be associated to photons.

what is the relationship between the electric field and the probability amplitude?

Photon state is described by the so-called Fock states or its linear combination. Whereas the electric field, since it's a physical quantity, is associated with a field operator $\tilde{E}$ and the electric field you observe is the average value of this operator with respect to the particular state of the photon, i.e. $\langle \psi | \tilde{E} | \psi\rangle$. The state $|\psi\rangle$ can take a number of forms, each of which is a particular linear combination of Fock states, for example number state, coherent state, squeezed state, etc, and again they do not have position representation.

 

[tade]

What about this? https://en.wikipedia.org/wiki/Riemann–Silberstein_vector

What does the bold p in the Schrödinger equation for the photon represent? Momentum?