bowlbase
- 145
- 2
Homework Statement
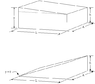
The shape is 3D trapezium with a base A and a length L. The front end is shorter than the back. The front is height h and the back height Y.
What is the resistance of a current moving from h to Y?
Homework Equations
R=ρL/A
The Attempt at a Solution
First to determine the area:
\frac{z-y}{x}
z=\frac{x}{L} (y-h)+h
That times A (the base) gives area
The integral:
\int \frac{\rho dx}{A\frac{x}{L} (y-h)+h}
evaluated from 0 to L I get:
\frac{\rho L}{A(y-h)} ln(\frac{y}{h})
This seems straight forward but I have a problem. The next step of the problem asks that I set the limit of y to zero so that the previous solution will give the resistance of a rectangular solid. This doesn't seem to work as the first half will be negative and the natural log becomes undefined.
I'm not sure that the integral is correct as my calculator, wolfram alpha and myself get differing answers. Though I think I made a mistake that puts me on wolframs side now. Also, the equation for the area may be incorrect though I am pretty sure that I got it correct.
Any assistance would be appreciated.