SRForum
- 6
- 0
Hello,
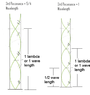
My teacher and the textbook seem to be conflicting with each other, and I would like to know who's right. The image on the left was scanned streight out my my textbook, saying that the third resonance is 5/4 lamda. On the right, is an edited version of the textbook image,showing what my teacher had showed me to display the third resonance in an air coloum. He calims that it's 1 lamda. Who's right? or are they both right? Thanks in advance for any help!
http://img428.imageshack.us/img428/9123/resonance8hc.png
My teacher and the textbook seem to be conflicting with each other, and I would like to know who's right. The image on the left was scanned streight out my my textbook, saying that the third resonance is 5/4 lamda. On the right, is an edited version of the textbook image,showing what my teacher had showed me to display the third resonance in an air coloum. He calims that it's 1 lamda. Who's right? or are they both right? Thanks in advance for any help!
http://img428.imageshack.us/img428/9123/resonance8hc.png
Last edited by a moderator: