Rico
- 2
- 0
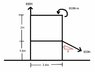
Determine the resultant R and the point on the y-axis through which the line of action of the resultant of the loading system shown passes
I have attached an image of the problem
In my attempt to solve the problem I went about the following steps:
1- I chose my axis to be right in the middle of the 2.4m length along the x axis
2 - Found the x and y components of the resultant force, as well as the magnitude of the resultant and its direction. Rounded off this equaled R = 755.43N and θ = 44.73°
3 - I got lost along this point now: I chose to find out the Resultant x moment and the resultant y moment excluding the moment of 800Nm already given.
4 - I then chose to find resultant moment of the problem by adding the resultant x with the resultant y and then finally adding the 800Nm moment
5 - I then got and answer of - 1340.64... Nm and now I needed to find its position along the y axis, correct? From here I do not know what to do.
Do we make this equation equal to a component of the resultant already worked out or just the resultant. The answer is meant to be 1.31m=y but I can't seem to get this answer.
I have attached an image of the problem
In my attempt to solve the problem I went about the following steps:
1- I chose my axis to be right in the middle of the 2.4m length along the x axis
2 - Found the x and y components of the resultant force, as well as the magnitude of the resultant and its direction. Rounded off this equaled R = 755.43N and θ = 44.73°
3 - I got lost along this point now: I chose to find out the Resultant x moment and the resultant y moment excluding the moment of 800Nm already given.
4 - I then chose to find resultant moment of the problem by adding the resultant x with the resultant y and then finally adding the 800Nm moment
5 - I then got and answer of - 1340.64... Nm and now I needed to find its position along the y axis, correct? From here I do not know what to do.
Do we make this equation equal to a component of the resultant already worked out or just the resultant. The answer is meant to be 1.31m=y but I can't seem to get this answer.