williamcarter
- 153
- 4
Hi,
Our lecturer explained us the Reynold Transport theorem, its derivation , but I don't get where the - sign in control surface 1 comes from? He said that the Area goes in opposite direction compared with this system.
I can't visualise this on our picture.
Can you please help me understand why we have the negative sign on the control surface 1 and at the end of the theorem we have +ve everywhere?
The pictures are attached below
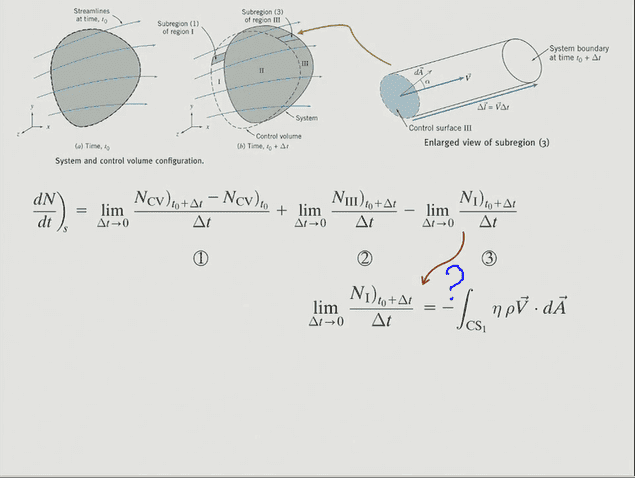
Fig1-Illustrates the - sign enquiry with regards to control surface 1. Why is it - here? and not +
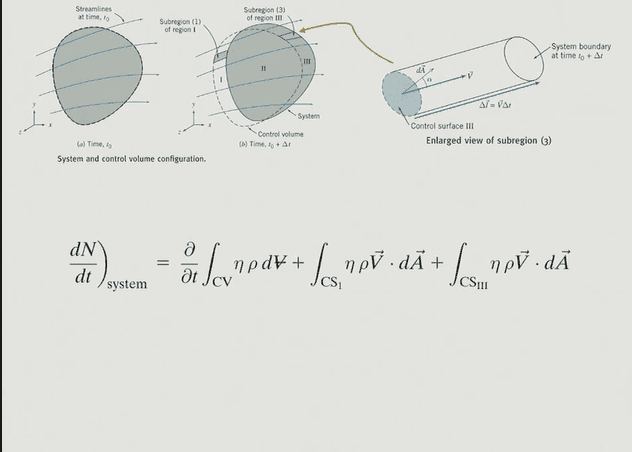
Fig2-Illustrates the final form of the Reynolds Transport theorem where all signs are +, why?How to know when the Area is in same direction as the system velocity ? and how to know when the Area goes opposite direction with regards to the system velocity?
Thank you in advance.
Our lecturer explained us the Reynold Transport theorem, its derivation , but I don't get where the - sign in control surface 1 comes from? He said that the Area goes in opposite direction compared with this system.
I can't visualise this on our picture.
Can you please help me understand why we have the negative sign on the control surface 1 and at the end of the theorem we have +ve everywhere?
The pictures are attached below
Fig1-Illustrates the - sign enquiry with regards to control surface 1. Why is it - here? and not +
Fig2-Illustrates the final form of the Reynolds Transport theorem where all signs are +, why?How to know when the Area is in same direction as the system velocity ? and how to know when the Area goes opposite direction with regards to the system velocity?
Thank you in advance.
Last edited: