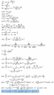To clarify, both DC sources in the circuit are step inputs? If so, you need to represent them as a heaviside function in the s-domain (or u_0(t)), like I did in the previous derivation. Though, I do have the sneaking suspicion that you are incorporating these into the circuit to account for the initial conditions that are obligatory for Laplace analysis; if so - don't! This will needlessly convolute the circuit - and your analysis.
As for the charged capacitor, you will have to represent it as either a current source or a voltage source in your analysis - I'm not sure which. Even though you are investigating the transient response, this will need to be expressed as a non-constant voltage function of time. This will be tough, since the Thevenin or Norton voltage equivalent of the capacitor will have an RLC impedance. When the long weekend comes around, I will try to find the answer for both of us. Also, is the charge on the capacitor representative of the initial conditions or an actual charge accumulation on the plates?
You'll have to determine the roots of the cubic using the general form of the roots for a cubic equation, as show in the Roots of a Cubic Function section here:
http://en.wikipedia.org/wiki/Cubic_function. Since you have variable coefficients, I believe that this is the only way to solve for it. I could be wrong, though. A more practical method is to substitute actual component values into the transfer function and solve.
With that being said, this method is quite tedious and very time consuming. Moreover, you are extremely likely to make a mistake. Perhaps you should build the circuit and analyze its response yourself? Otherwise, there is a panoply of engineering software out there that can expedite your analysis.
I would help more, but I have my own Engineering coursework to struggle with!