Rolling Object, Moving Incline

[BryMan92]

Homework Statement

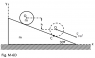
A right triangular prism ABD with inclination angle 30degrees and mass m can slide without friction along smooth horizontal surface. A uniform solid cylinder of mass m rolls down the inclined surface AB without friction. If both cylinder and prism are at rest initially, what will be the relative velocity and absolute velocity of the cylinder’s center O after its height decreased by h?

Hints: 1. You may use conservation of momentum principle for the system cylinder-prism to relate velocities of prism and of cylinder’s center (absolute and relative )
2. When you apply conservation of energy relation do NOT forget to account for kinetic energy of the cylinder’s rotation.

Homework Equations

Pe=mgh
KE = 1/2Iω^2 and 1/2mv^2
m1v1=m2v2
Vabs = Vrel-Vprism

The Attempt at a Solution

2gh=V^2 +V^2+Vprism^2

MsystemVprism=MSystem(Vrel(i)-Vprism)
Vprim=((Vrel√3)/4) - My professor said this was correct.

So, this is where I get stuck because I am not sure which V to use for the rotational energy or the translational energy. I tried using Vrel for everything and I get the wrong answer. I think I am suppose to use Vabsolute for the velocities of the cylinder, but that gives me some ugly math which I think is wrong.

Any help would be helpful, and I really appreciate it!

 

[tiny-tim]

Hi BryMan92!

… I am not sure which V to use for the rotational energy or the translational energy. I tried using Vrel for everything and I get the wrong answer. I think I am suppose to use Vabsolute for the velocities of the cylinder, but that gives me some ugly math which I think is wrong.

Newtonian mechanics (including conservation of energy or momentum) only works in an inertial frame.

The prism is not an inertial frame, so yes, you have to use the lab frame.

(it shouldn't be too difficult: v_cylinder = v_relative + v_prism )

 

[writ]

Can anyone give further help on this problem? I'm pretty confused, since our professor told us in hints to use the energy approach, but now it is being said that this isn't valid?