my bad. I mistakenly wrote "wouldn't", when it should have been "would".
The correct statement is: If the mass distribution doesn't change just because the ball is rotating, this means the moment of inertia should not change just because the ball is rotating. If so, why would the moment of inertia of a ball rotating about its own axis and also simultaneously about an axis passing through C, change from that calculated when it wasn't rotating at all.?
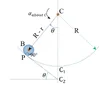
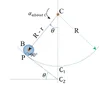
This is what I mean: In this pic(Pic 1 below), when the ball is just lying at the bottom most point on the concave surface and is not rotating at all, the moment of inertia of the ball about the axis passing through point C, and perpendicular to the page, is = ##\frac{2}{5}mr^{2} + m \left ( R-r \right )^{2} ##. I suppose you'll agree up to this point. In this situation, perpendicular axis theorem for calculation of moment of inertia has been correctly applied. I suppose you'll agree to this too.
View attachment 366237
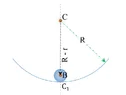
However, now take a look at this pic(Pic 2 below), when the ball is rotating about an axis passing through it's own centre of mass, i.e. point B and perpendicular to the page, and also simultaneosuly rotating about an axis passing through the point C(centre of curvature of concave surface) and is perpendicular to the page.
View attachment 366238
According to
@haruspex's comment in post#26:
and in post#33
But in your post#42, you've clearly mentioned that:
meaning that calculation of moment of inertia is NOT dependent on whether the body is rotating or not.
So, what I gather from these posts is that
@haruspex is saying is that the 2 conditions(shown in the 2 pics above) are different even regarding the calculation of moment of Inertia. According to him, the moment of Inertia in the 2nd case(when the ball is rotating about 2 axes simultaneously), is NOT = ##\frac{2}{5}mr^{2} + m \left ( R-r \right )^{2} ##. This is what I don't understand, since in post#40, he does agree that mass distribution doesn't change just because the ball is now rotating. And moment of inertia is just a measure of how the mass is distributed about an axis. So my contention is that in this 2nd case too, the moment of Inertia of the ball about the axis passing through point C and perpendicular to the page should be = ##\frac{2}{5}mr^{2} + m \left ( R-r \right )^{2} ##.
Appreciate the point-wise refresher course on how to calculate moment of inertia. However, I already know that and that's not what I was asking for.
I want to know what will be the moment of Inertia of the ball about the axis passing through the point C and perpendicular to the page, in the case when the ball is rotating about 2 axes simultaneously(as shown in Pic 2). In my opinion, it should be = ##\frac{2}{5}mr^{2} + m \left ( R-r \right )^{2} ##.