Rotating and Nonrotating Rods Superposed

[PeachBanana]

Homework Statement

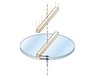
A uniform disk turns at 3.7 rev/s around a frictionless spindle. A nonrotating rod, of the same mass as the disk and length equal to the disk's diameter, is dropped onto the freely spinning disk . They then both turn around the spindle with their centers superposed. What is the angular frequency in rev/s of the combination?

Homework Equations

L = Iω

The Attempt at a Solution

I was trying to relate the angular velocity to this but I don't think that's the correct approach. For example, on my second attempt I had:

ω = L / (1/6)(M)(l)^2

(3.7 rev/s)(6) = 22.2 rev/s

I'm having trouble finding a connection.

 

[gneill]

Think inelastic collision angular style!

 

[PeachBanana]

I'll try to explain this without it turning into a complete mess. I still thought of L = Iω and assumed it would be conserved. I made two equations:

L = (1/12)Mr^2 * 3.7 rev./s

L = ((1/12)Mr^2 + (1/12)Mr^2) * ω

So then I tried to make a proportion.

L1 / L2 = 0.30833 rev./s * Mr^2
---------------------
(1/6 Mr^2) * ω6 Mr^2 * ω L1 = L2 * 0.30833 rev./s * Mr^2

ω = L2 * 0.30833 rev./s * Mr^2
---------------------------
L1 * 6 Mr^2

I assumed momentum was conserved which I why I though L2 and L1 canceled. For ω, I got 5.138 * 10 ^-2 rev./s which doesn't make a lot of sense.

 

[gneill]

I'll try to explain this without it turning into a complete mess. I still thought of L = Iω and assumed it would be conserved. I made two equations:

L = (1/12)Mr^2 * 3.7 rev./s

L = ((1/12)Mr^2 + (1/12)Mr^2) * ω

One problem here: the expression for the moment of inertia of a disk is not the same as that of a thin rod. Use the expression for a disk to determine the system's angular momentum. Use a common measure for the radius of the disk and the length of the rod (so if the disk's radius is r, then the rod's length is 2r).

So then I tried to make a proportion.

L1 / L2 = 0.30833 rev./s * Mr^2
---------------------
(1/6 Mr^2) * ω


6 Mr^2 * ω L1 = L2 * 0.30833 rev./s * Mr^2

ω = L2 * 0.30833 rev./s * Mr^2
---------------------------
L1 * 6 Mr^2

I assumed momentum was conserved which I why I though L2 and L1 canceled. For ω, I got 5.138 * 10 ^-2 rev./s which doesn't make a lot of sense.

You won't need to make a proportion if you simply equate the expression for the angular momentum after collision to the expression before. You should find that in solving for the new angular velocity that a LOT of stuff is going to cancel out

 

[PeachBanana]

Ok. I think I have this figured out.

The initial moment of inertia is just the disk. 1/2 Mr^2.
Once the disk is added, the final moment of inertia is 1/12 M (2r)^2 + 1/2 Mr^2 = 5/6 Mr^2.

So now I can make an equation relating the two:

3.7 rev./s (1/2 Mr^2) = 5/6 Mr^2 * ω
ω final ≈ 2.2 rev./s

 

[gneill]

Ok. I think I have this figured out.

The initial moment of inertia is just the disk. 1/2 Mr^2.
Once the disk is added, the final moment of inertia is 1/12 M (2r)^2 + 1/2 Mr^2 = 5/6 Mr^2.

So now I can make an equation relating the two:

3.7 rev./s (1/2 Mr^2) = 5/6 Mr^2 * ω
ω final ≈ 2.2 rev./s

That looks much better!