Rotation - Collision of Rotating Cylinders Cylinders

[cupid.callin]

Homework Statement

The Attempt at a Solution

The book did it like taking impulse of forces f and writing eqn Impulse = Δ(Angular momentum)
or J = ΔL

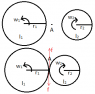
How i tried:

let the 2 cylinders meet at A

(they have not mentioned the velocity of approach but as it says that the 2 cylinders remain in contact and don't fly off after collision so i guessed that velocity is negligible)

Considering Torque at A
As no torque acts during whole process so L about A remains constant

L_{initial} = I_1w_1 \ - \ I_2w_2

now let that after they meet and friction does it work they have angular speeds w₁' and w₂'

L_{final} = I_1w_1' - I_2w_2'

and also

w_1'r_1 = w_2'r_2
as the point of contact of 2 cylinders has same velocity

But this gives wrong answer!

Can someone tell me why this method is wrong?

 

[tiny-tim]

hi cupid.callin!

your method should work

can i check … when you said …

As no torque acts during whole process so L about A remains constant

… did you calculate L using the moments of inertia about the centres (which is correct), or about A (which isn't) ?

 

[cupid.callin]

… did you calculate L using the moments of inertia about the centres (which is correct), or about A (which isn't) ?

moment if inertia of a body about any point,

\vec{L} = \vec{L}_{CM} + m\vec{r}X\vec{v}_o

where v_o is velocity of CM

And as i said that cylinders do not fly away after collision, v_o ≈ 0

So

\vec{L} = \vec{L}_{CM}

 

[cupid.callin]

And if the torque about A is zero then shouldn't momentum be conserved about A and thus calculate moments of inertia about A ?

If i calculate moments of inertia along CM then the friction will have torque and then momentum is not conserved !

 

[tiny-tim]

hi cupid.callin!

\vec{L} = \vec{L}_{CM}

yes, that's right …

L_A = L_c.o.m.

but you said you used the formula Iω for L_A, so i was just checking whether you used I_Aω or I_c.o.m.ω

 

[SammyS]

What form is the answer in?

Can you show your solution?