Rotation of rigid bodies: yo-yo

[syang9]

consider a yo-yo consisting of two cylinders of radius R1, (combined) mass M1, glued to another smaller cylinder of radius R2, mass M2. find the final velocity after falling a height h using Newton's second law. assume the string is vertical.

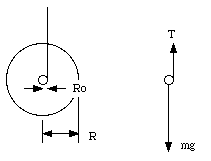
the inner radius R2 is R0, the outer radius R1 is R in this picture

so, i started off by applying f = ma to M2..

Fnet, y = (M1 + M2) - T = (M1 + M2)(a)cm

tnet, ext = T(R1) = I(alpha), alpha = (a)cm/R1

i calculated the moment of inertial to be the sum of the moments of inertia of the cylinders..

I = 1/2*(M1*R1^2 + M2*R2^2)

solving for (a)cm, i get a very nasty formula..

a = (M1 + M2)g / ( ( I/(2R1^2)) + (M1 + M2))

my original plan was to integrate this wrt time to get a velocity.
but this formula doesn't involve anything that changes with time.. so how do i obtain the final velocity? am i even on the right track?

 

[Fermat]

It looks ok.
As you noticed, the expression for a doesn't involve anything that changes wrt time. In other words, a is constant!

If you had an object that was falling under gravity, what would its velocity be after having fallen a distance h?

So then, what if g = a?