blueblast
Hey guys,
I'm having trouble understanding this problem that was on an AP Physics 1 sample questions page:
 So a couple of questions here:
So a couple of questions here:
(By the way, I know the answer is C)
1. My teacher explained that the net torque here on the assembly would be zero(will ask him again later). Is this because the torque was already applied at one point in time, and now the two masses are not accelerating?
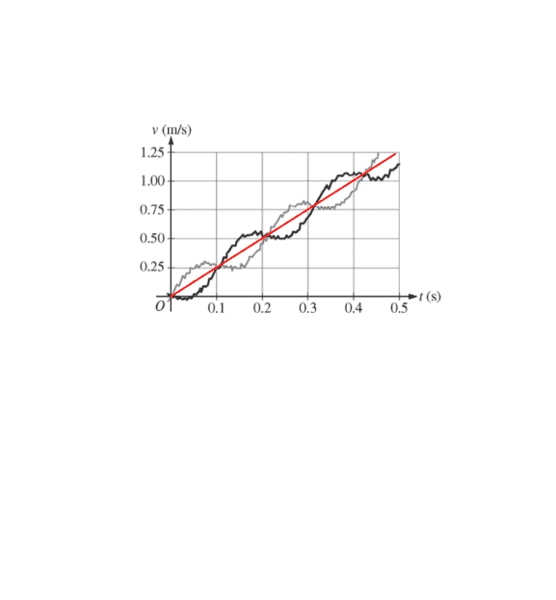
2. Why does the graph have curves? Does it have to do with gravity changing the speed of the masses?
What I do know is the acceleration of the COM straight down, due to gravity. This can be found by the points on the graph that meet:
It would be awesome if you guys could help me out :)
I'm having trouble understanding this problem that was on an AP Physics 1 sample questions page:
(By the way, I know the answer is C)
1. My teacher explained that the net torque here on the assembly would be zero(will ask him again later). Is this because the torque was already applied at one point in time, and now the two masses are not accelerating?
2. Why does the graph have curves? Does it have to do with gravity changing the speed of the masses?
What I do know is the acceleration of the COM straight down, due to gravity. This can be found by the points on the graph that meet:
It would be awesome if you guys could help me out :)