Rotational Collisions: Putty Wad

[ledphones]

Homework Statement

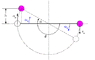
Two 2.1 kg balls are attached to the ends of a thin rod of negligible mass, 63 cm in length. The rod is free to rotate in a vertical plane about a horizontal axis through its center. With the rod initially horizontal as shown, a 50 gm wad of wet putty drops onto one of the balls with a speed of 3.9 m/sec and sticks to it. a) What is the angular speed of the system just after the putty wad hits?

ω = rad/sec *
.146 OK

b) What is the ratio of the kinetic energy of the entire system just after the collision to just before the collision?

KEafter/KEbefore = *
.01175 OK

c) Through what angle will the system rotate until it momentarily stops?

ΔΘ = rad

Homework Equations

The Attempt at a Solution

Im not sure how to approach part c since I don't know the acceleration or the time it takes to stop.

 

[gneill]

Have you thought about using a conservation of energy approach?

 

[ledphones]

how would you use that to solve for the angle? would you have
K+U=K+U
1/2 I w^2 + 0 = 0 + ? what would the potential energy be here? and how could you relate it to the angle (or distance traveled?) would it be through a kinematic equation?

 

[gneill]

how would you use that to solve for the angle? would you have
K+U=K+U
1/2 I w^2 + 0 = 0 + ? what would the potential energy be here? and how could you relate it to the angle (or distance traveled?) would it be through a kinematic equation?

Consider that the rod and balls without the wad of putty are symmetrical, so that they would be in equilibrium at any angle. No change in PE occurs if its angle is changed. If it were set rotating, it would do so at a constant velocity (barring friction, of course).

The wad sticking to one end changes things. There will be a PE associated with its relative height. It's the only part of the system for which a net exchange of energy with the gravitational field will occur.

 

[ledphones]

so you'd know the potential energy once the wad hits is (m+M)gh. so i'd set that equal to 1/2 Iw^2 and solve for h. but this was a value of .0002133 which is much to small.

 

[gneill]

so you'd know the potential energy once the wad hits is (m+M)gh. so i'd set that equal to 1/2 Iw^2 and solve for h. but this was a value of .0002133 which is much to small.

Why m+M?

 

[ledphones]

i tried just M now. and that was wrong as well. as for my reason for adding those two i though you had to add the mass of the wad of gum plus one of the balls

 

[gneill]

i tried just M now. and that was wrong as well. as for my reason for adding those two i though you had to add the mass of the wad of gum plus one of the balls

I see. Well, as I said, the rod and balls are symmetrical, so their contribution is nil except that they add to the moment of inertia of the whole.

You'll have to show your calculation, reasoning, and numbers if we're to see what's going wrong.

 

[ledphones]

ok so i tried:
1/2(MR^2+MR^2+mr^2)w^2=mgh
h=(.5(2*2.1*.351^2+.050*.351^2)*.146^2)/(.05*9.8)

 

[gneill]

ok so i tried:
1/2(MR^2+MR^2+mr^2)w^2=mgh
h=(.5(2*2.1*.351^2+.050*.351^2)*.146^2)/(.05*9.8)

Okay. The rod has length 63cm, so the radius is 0.315m. I think you've got a typo there where you've used 0.351.

The height that's calculated will be the distance above the initial height (rod horizontal) that the wad must reach. Immediately after impact the wad is heading downward and picking up speed, maxing out at the bottom of its arc. It then proceeds up the other side, losing speed, until the rod is once again horizontal and the speed is the same as the initial speed, and the KE is the same as the initial KE. After this it continues upwards until it reaches height h above the horizontal.

 

[ledphones]

Ok so now I tried

1/2Mv^2/r^2=Mgh

h=.5(2.1)(3.9^2)/(.315^2*9.81*2.1)

this was wrong :(

 

[gneill]

Ok so now I tried

1/2Mv^2/r^2=Mgh

h=.5(2.1)(3.9^2)/(.315^2*9.81*2.1)

I don't know what to make of that; the units on the LHS of the first expression don't come out as energy. What's the equation meant to describe?

 

[gneill]

Let's go back to what is known. What value did you calculate for the KE immediately after the collision?

 

[ledphones]

.0044945452(from the following expressions:)

1/2Iw^2
I=(2*MR^2+mR^2)

 

[gneill]

.0044945452(from the following expressions:)

1/2Iw^2
I=(2*MR^2+mR^2)

Okay. That's about what I calculate: 4.474 x 10^-3 J. I suppose I'm keeping a few more decimal places in all the intermediate results.

Now, the ball with the wad travels around in its arc attached to the rod end until the rod is once again horizontal. That's an angle of pi radians so far traveled. At this point the system has the same KE as it had when the wad of putty first struck. As the wad rises above the horizontal, the system loses KE to gravitational PE.

So how high must the wad of putty rise in order to "steal" all of the rotational KE?

h = KE/(m*g)

What value do you get for h and the resulting angle above horizontal? (an angle which must be added to the angular distance already traveled by the ball and wad).