Juniper7
- 19
- 0
Homework Statement
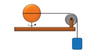
A solid sphere of mass 6.0 kg is mounted on a vertical axis and can rotate freely without friction. A massless cord is wrapped around the middle of the sphere and passes over a 1.0 kg pulley and is attached to a block of mass 4.0kg. What is the speed of the block after it has fallen 80 cm? Treat the pulley as a sold cylinder.
Homework Equations
I of a solid cylinder = 1/2MR2
I of a sphere = 2/5MR2
KErotational = 1/2Iω2
KElinear = 1/2mv2
PE = mgh
ω = v/r
The Attempt at a Solution
I am very lost in this question. I have tried to calculate the kinetic energies of each part of the system but it doesn't give radii or ω so I get stuck. I thought this could be relevant:
KEsphere + KEpulley + KEblock
But what would I equate those energies to? Thank you in advance for any help!
Attachments
Last edited: