Find the velocity and acceleration of a pulley in a mass-spring system

[mattlfang]

Homework Statement

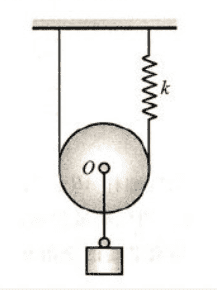
Given below system. We know the Hooke's constant of the spring is k. the mass of the box under the pulley is m. The mass of the pulley is M. The radius of the pulley is R. Radius of gyration is r

We release the system from the static state. When the spring is extended by L, what's the the velocity and acceleration of the pulley?

Relevant Equations

Radius of gyration, moment of inertia, conservation of energy

This looks like a classical setup but I can't find a solution. We can calculate the energy of the system by looking at the work done by the gravity and the spring. But how do we divide the energy between the kinetic energy of the pulley and the rotation of the pulley?

 

[haruspex]

how do we divide the energy between the kinetic energy of the pulley and the rotation of the pulley?

By assuming the string does not slip on the pulley. What relationship does that give you between the rotational velocity and the vertical velocity of the pulley’s centre?

 

[Delta2]

Sorry I want to ask something, is radius of gyration the length of the string that connects the center of the pulley to the small mass?

 

[haruspex]

Sorry I want to ask something, is radius of gyration the length of the string that connects the center of the pulley to the small mass?

No, it means the distance k s.t. moment of inertia is mk².

 

[Delta2]

So, @haruspex this problem can be solved with energy considerations only or we ll have to do it with forces and solve differential equations? Something tells me because it asks for the acceleration we have to do it with forces is that correct?

 

[haruspex]

So, @haruspex this problem can be solved with energy considerations only or we ll have to do it with forces and solve differential equations? Something tells me because it asks for the acceleration we have to do it with forces is that correct?

The velocity can be found by considering energy, the acceleration by considering forces. Neither requires calculus.

 

[Delta2]

Neither requires calculus

So I guess the acceleration of the system is constant? Somehow I thought the acceleration would be time varying (the system doesn't look that simple, the tension and the spring force should be time varying) that's why I thought we would have to solve differential equation.

 

[Delta2]

Let me answer my own question, the acceleration will be time varying but it only asks for the acceleration when spring is extended by L, not for the full function a(t).

 

[Leo Liu]

So what would be the solution to this problem? I am curious.

 

I hope I understood it right now

Spoiler

Let $y$ be the downward distance traveled by the configuration from its starting position, let the tension in the string on the left be $T$ (and since the pulley must be frictional in order to satisfy the "no-slip" condition, this tension will be different to that on the right hand side, which is $k[2y]$). Let the angular speed of the disk about its centre be $\omega$. When the configuration descends one unit, the spring stretches by two units.We can write down 4 equations:$$\begin{align*}

\text{Energy} &: 0 = \frac{1}{2} (M+m)\dot{y}^2 + \frac{1}{2}I \omega^2 + \frac{1}{2}k(2y)^2 - (M+m)gy \\ \\

\text{Newton II} &: (M+m)g - T - k(2y) = (M+m)\ddot{y} \\ \\

\text{Torques about CM} &: TR - k(2y)R = I\dot{\omega} \\ \\

\text{"No-slip" condition} &: \dot{y} = \omega R \implies \ddot{y} = \dot{\omega} R



\end{align*}$$And also let $I \equiv Mr^2$, as noted earlier.

 

[Leo Liu]

Let $y$ be the downward distance traveled by the configuration from its starting position, let the tension in the string on the left be $T$ (and since the pulley must be frictional in order to satisfy the "no-slip" condition, this tension will be different to that on the right hand side, which is $k[2y]$). Let the angular speed of the disk about its centre be $\omega$. When the configuration descends one unit, the spring stretches by two units.We can write down 4 equations:$$\begin{align*}

\text{Energy} &: 0 = \frac{1}{2} (M+m)\dot{y}^2 + \frac{1}{2}I \omega^2 + \frac{1}{2}k(2y)^2 - (M+m)gy \\ \\

\text{Newton II} &: (M+m)g - T - k(2y) = (M+m)\ddot{y} \\ \\

\text{Torques about CM} &: TR - k(2y)R = I\dot{\omega} \\ \\

\text{"No-slip" condition} &: \dot{y} = \omega R \implies \ddot{y} = \dot{\omega} R



\end{align*}$$And also let $I \equiv Mr^2$, as noted earlier.

Brilliant. I didn't get the equation which relates $\omega$ to $\dot y$, and $\Delta x_{spring}=2\Delta y$. Although my intuition tells me the second equation (x=2y) is true, could you prove it algebraically?

 

Here's a way to think about it...

cut the string at two points at the same height on either side, then move the lower piece of the system down a distance $y$. To fill the two gaps you made in the string, you insert two more bits of string each of length $y$ into the gaps, one for each gap.

 

[Leo Liu]

Okay I think I have proved it: $y=1/2(l-\pi R)\implies |\Delta y|=|y-0|=1/2 [(l'-\pi R)-(l-\pi R)]=1/2(l'-l)=1/2 \Delta x_{spring}$, where l' is length after, I is the length before, y is the distance from the point of attachment to the CM of the wheel.

As regards the angular speed of the wheel, the angle it rotates during a period multiplied by the radius is equal to the increase in the length of the distance from the point of attachment to the point where the string contacts the left side of the pulley ($\theta R=h_1$), and we label this distance as $h_1$. It is easy to see that $\dot h_1=\dot y$, so $\omega R=\dot y$.

My obsession with rigor have blinded me to the big picture.

 

I think you could simplify that, by saying just that the rate at which the spring extension increases is equal to the rate at which the total length of the cord increases. This must clearly hold, since if $L = L_0 + \delta$, then $dL/dt = d\delta/dt$. If the configuration moves down by a distance $d$ in some time interval $\delta t$, the total length of the cord increased by an amount $2d$.

 

[mattlfang]

Thanks guys for your help, I think I figured it out ..