salleyye
- 2
- 0
Hi,
I have a physics assignment due, and I've been struggling with a particular question. I would really appreciate if anyone could please help.
Consider the system below. The mp = 20.0 kg 'pulley' is a solid uniform sphere of radius of 0.250 m with the frictionless axle passing through its diameter. The mass of the block on the incline is m1 = 16.0 kg, and the coefficient of kinetic friction between the two blocks and the surfaces is μK = 0.220. (Assume the pulley’s axle is frictionless, and that the rope slides over the pulley without slipping.)
Use energy methods to find the speed of the blocks after they have moved 2.20 m from rest.
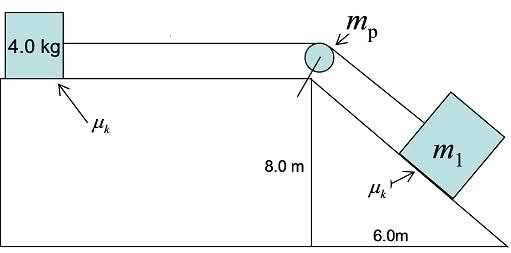
In my solution, I use x to refer to the displacement of each block (2.20 m), y0 to be the initial height of block 1, and y1 to be the final height of block 1.
Wnc = ΔEf - ΔE0
EK = (1/2)mv2
EK = (1/2)Iω2
Iuniform sphere = (2/5)MR2
EP = mgh
Wfriction = -μKNd = -μKmgd
Putting together all the above equations, I came up with the following:
Wnc = ΔEf - ΔE0
-μKm1gx(sinθ) - μKm2gx = m1gy1 + (1/2)m1v2 + (1/2)m2v2 + (1/2)Iω2 - m1gy0
-μKgx(m2 + m1sinθ) = m1g(y1 - y0) + (1/2)v2(m1 + m2) + (1/2)(2/5)(mpR2)ω2
From the given information, y1 - y0 = -x(sinθ). Also, because the rope does not slip, then R2ω2 = v2. Based on this information, the equation becomes:
-μKgx(m2 + m1sinθ) = -m1gx(sinθ) + (1/2)v2(m1 + m2) + (1/5)mpv2
Substituting in the values, we get:
(-0.220)(9.81 m/s2)(2.20 m)[4.0 kg+(16.0 kg)(0.8)] = -(16.0 kg)(9.81 m/s2)(2.20 m)(0.8) + (1/2)v2(20 kg) + (1/5)(20.0 kg)v2
-79.767072 (m2/s2)kg = -276.2496 (m2/s2)kg + (14.0 kg)v2
v = 3.75 m/s
Unfortunately, my solution is incorrect... yet I have no idea where I went wrong. Can someone please help? Thanks.
I have a physics assignment due, and I've been struggling with a particular question. I would really appreciate if anyone could please help.
Homework Statement
Consider the system below. The mp = 20.0 kg 'pulley' is a solid uniform sphere of radius of 0.250 m with the frictionless axle passing through its diameter. The mass of the block on the incline is m1 = 16.0 kg, and the coefficient of kinetic friction between the two blocks and the surfaces is μK = 0.220. (Assume the pulley’s axle is frictionless, and that the rope slides over the pulley without slipping.)
Use energy methods to find the speed of the blocks after they have moved 2.20 m from rest.
In my solution, I use x to refer to the displacement of each block (2.20 m), y0 to be the initial height of block 1, and y1 to be the final height of block 1.
Homework Equations
Wnc = ΔEf - ΔE0
EK = (1/2)mv2
EK = (1/2)Iω2
Iuniform sphere = (2/5)MR2
EP = mgh
Wfriction = -μKNd = -μKmgd
The Attempt at a Solution
Putting together all the above equations, I came up with the following:
Wnc = ΔEf - ΔE0
-μKm1gx(sinθ) - μKm2gx = m1gy1 + (1/2)m1v2 + (1/2)m2v2 + (1/2)Iω2 - m1gy0
-μKgx(m2 + m1sinθ) = m1g(y1 - y0) + (1/2)v2(m1 + m2) + (1/2)(2/5)(mpR2)ω2
From the given information, y1 - y0 = -x(sinθ). Also, because the rope does not slip, then R2ω2 = v2. Based on this information, the equation becomes:
-μKgx(m2 + m1sinθ) = -m1gx(sinθ) + (1/2)v2(m1 + m2) + (1/5)mpv2
Substituting in the values, we get:
(-0.220)(9.81 m/s2)(2.20 m)[4.0 kg+(16.0 kg)(0.8)] = -(16.0 kg)(9.81 m/s2)(2.20 m)(0.8) + (1/2)v2(20 kg) + (1/5)(20.0 kg)v2
-79.767072 (m2/s2)kg = -276.2496 (m2/s2)kg + (14.0 kg)v2
v = 3.75 m/s
Unfortunately, my solution is incorrect... yet I have no idea where I went wrong. Can someone please help? Thanks.
