chemica1mage
- 3
- 0
Hi,
The question I have is not for a numerical answer but for clarification.
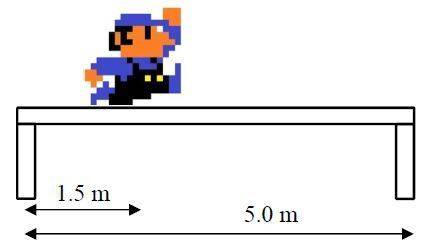
Some of the questions involving torque/rotational equilibrium describe a person standing on a plank. I know that the gravitational force of the person on the plank needs to be considered for translational and rotational equilibrium. My question is, why don't I consider the normal force exerted by the board on the person as a torque-producing force? (Your typical dynamics situation where F(normal) = F(gravity).) Or is it because the "normal force" is distributed between the two supports.
Any help on this question is greatly appreciated!
The question I have is not for a numerical answer but for clarification.
Some of the questions involving torque/rotational equilibrium describe a person standing on a plank. I know that the gravitational force of the person on the plank needs to be considered for translational and rotational equilibrium. My question is, why don't I consider the normal force exerted by the board on the person as a torque-producing force? (Your typical dynamics situation where F(normal) = F(gravity).) Or is it because the "normal force" is distributed between the two supports.
Any help on this question is greatly appreciated!