Contradiction between Torque and Linear Motion in Rolling Motion

[zorro]

Homework Statement

Suppose a uniform sphere of mass M and radius R is placed on a rough horizontal surface. It rolls without slipping.

We can apply 2 equations.
1) considering the torque due to frictional force about the centre of mass,
fR=I(alpha)
here alpha=a/R as the it is in pure rolling motion
so f=2Ma/5

2)considering the linear motion,
Ma=f

why are 1 and 2 contradicting.?

 

[hikaru1221]

Well, they're not. Why? f=0 and a=0. No contradiction, right?
Think of energy conservation law. If the ball rolls without slipping on a HORIZONTAL surface, without any force from us, does the ball accelerate?

 

[zorro]

Ok fine.
Suppose the ball is moving with uniform velocity (without any acceleration and any sliding motion).
As you told f=0.
Then what causes the ball to rotate? there must be some sliding friction right?

 

[hikaru1221]

Ok fine.
Suppose the ball is moving with uniform velocity (without any acceleration and any sliding motion).
As you told f=0.
Then what causes the ball to rotate? there must be some sliding friction right?

Let's look at initial conditions. When the ball rolls without sliding, that means the ball has both linear velocity v and angular velocity w=vR. Just like v, w doesn't change.
The force only causes the CHANGE in v and the torque only causes the CHANGE in w.
And how does the ball gain v and w? Maybe before you drop it on the ground, you spin it or hit it or so, as long as it gains v and w such that w=vR. But that's out of our concern. We only care what happens when the ball already rolls without sliding.

 

[zorro]

Alright its clear now.

I got another one.
A rod is released from vertical position (giving it a negligible small push) on a smooth horizontal surface. Is the direction of normal reaction perpendicular to the ground or along the rod when it is inclined at angle to the ground? Is there any radial acceleration during its motion?. Suppose the ground is rough (such that it does not allow slipping of bottom of the rod). Then will the above answers change?

P.S.- This doubt is a product of my mind which came while solving problems.

 

[hikaru1221]

A rod is released from vertical position (giving it a negligible small push) on a smooth horizontal surface. Is the direction of normal reaction perpendicular to the ground or along the rod when it is inclined at angle to the ground? Is there any radial acceleration during its motion?. Suppose the ground is rough (such that it does not allow slipping of bottom of the rod). Then will the above answers change?

What do you think? (sorry, forum's rule; I cannot answer before you provide some of your thoughts )

P.S.- This doubt is a product of my mind which came while solving problems.

Okay, that means you're getting better than the book you read / the problem your solved

 

[zorro]

Well, I think the direction of normal force is along the rod and there is centripetal acceleration in both the cases.

 

[hikaru1221]

Well, I think the direction of normal force is along the rod and there is centripetal acceleration in both the cases.

Why's that?

 

[zorro]

I don't have a clear explanation for it. May be because normal force always acts along the centre of mass of a body.
Centripetal acceleration is necessary for rotation.

 

[hikaru1221]

I don't have a clear explanation for it. May be because normal force always acts along the centre of mass of a body.
Centripetal acceleration is necessary for rotation.

1/ About the direction of normal force:
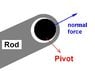
Actually the normal force ALWAYS acts perpendicular to the contacting surface. Ideally it should be a contacting point, not a surface. But the real situation is never like that. Instead of a rigid rod, you push your thumb on the ground and will see that it's a contacting surface.

So that's the same with the rod. When the width of the rod is so small compared to its length, you can model the rod as a straight line whose width = 0. But when it comes to normal force, we have to look at it carefully. See the attached picture. If you try to zoom it and zoom it and zoom it, you will see something like that: it's a contacting surface. Therefore the normal force acts perpendicular to the ground / the plane, not along the rod.

2/ About the centripetal acceleration:
When you mention centripetal acceleration (C.A.), you MUST refer to C.A. of which point. For example, if it's a rough surface and the lower end of the rod sticks to the ground, then the rod performs rotation about that end. Every point on the rod has its own C.A., except for the lower end: this end doesn't move, so it doesn't have C.A.

Likewise, in the case that the surface is smooth, the rod falls: the center of mass (COM) of the rod & the lower end of the rod perform motion in a straight line, so these 2 points don't have C.A., while other points perform "weird" motion (their orbits are neither circle nor straight line!), so these points have C.A.

 

[zorro]

That cleared the problem.

Suppose the rod is pivoted on a fixed support, then why do we take the normal force along the rod? it is not perpendicular to the surface here right?

about centripetal acceleration, consider this problem.

A thin rod is held resting on a rough ground with its length inclined at an angle (theta) to the horizontal. The coefficeint of friction between rod and ground is (mu). Show that when the rod is let go it will start slipping on the ground if (mu) < 3sin(theta)cos(theta)/(1+3sin^2(theta)

In this problem, if we consider the limiting case i.e. the rod is just about to slip then do we have to take any centripetal acceleration of centre of mass for calculating its net acceleration (tangential acceleration is also present)?
Since the centre of mass follows a circular path while falling, I calculated net acceleration of centre of mass including its centripetal acceleration but got wrong answer. (answer considers only tangential acceleration)
Why is it so?

 

[hikaru1221]

Suppose the rod is pivoted on a fixed support, then why do we take the normal force along the rod? it is not perpendicular to the surface here right?

I'm not sure what situation you are referring to, but maybe the attached picture can shed a little light. In the picture, the pivot is lubricated. If the pivot is not so smooth, there is friction, and the resultant force on the rod is no longer along the rod.

In this problem, if we consider the limiting case i.e. the rod is just about to slip then do we have to take any centripetal acceleration of centre of mass for calculating its net acceleration (tangential acceleration is also present)?

Yes. Just before the rod slides, COM still performs circular motion.

Since the centre of mass follows a circular path while falling, I calculated net acceleration of centre of mass including its centripetal acceleration but got wrong answer. (answer considers only tangential acceleration)
Why is it so?

Why don't you show me your work?

 

[zorro]

Why don't you show me your work?

Sure dear

considering the torque acting about the point of contact,
mgcos(theta) l/2=ml^2/3 (alpha)
from here,
tangential acceleration is 3gcos(theta)/4

Using conservation of energy,
mgl/2 (1-cos(theta))=0.5 ml^2/3 w^2
(taking reference level through the initial position of centre of mass)
from here i get w^2=3g(1-cos(theta))/l

centripetal acceleration of the centre of mass=mw^2 l/2
=3g(1-cos(theta))/2

now the frictional force balances the force due to centre of mass in x-direction
taking components of tangential and centripetal acceleration along x- direction I got one equation involving N-the normal force which is perpendicular to the ground. ( (mu)N=m(ax))

then taking components of accelerations along y-direction ,
mg-N=m(ay)

solving for N I did not get the right answer.
Instead if i proceed without considering centripetal acceleration of the centre of mass, I got the correct answer. How?

 

[hikaru1221]

There is one mistake here:
"mgl/2 (1-cos(theta))=0.5 ml^2/3 w^2 "
Anyway I also don't get the answer. What is the source of the problem?
It's midnight at my place so I'll come back to this tomorrow.

 

[zorro]

erm leave it if you don't get. You must be very busy with your first year
Source of this problem is my Physics book from Brilliant Tutorials for IIT-JEE (the toughest engineering entrance exam in the world )

 

[zorro]

What is the mistake there anyway?

 

[hikaru1221]

Ah, I read the question again and now I see where we were wrong. Staying up late is really horrible

A thin rod is held resting on a rough ground with its length inclined at an angle (theta) to the horizontal. The coefficeint of friction between rod and ground is (mu). Show that when the rod is let go it will start slipping on the ground if (mu) < 3sin(theta)cos(theta)/(1+3sin^2(theta)

The question doesn't mean that you hold and release the rod at the vertical position! The rod is first held at the (theta) position, then released. The question wants us to show that right after being released, the rod will slide if the above expression is satisfied. This is why there is no centripetal acceleration included: right after being released, the rod hasn't gained any speed yet, so centripetal acceleration at that time = 0!

erm leave it if you don't get. You must be very busy with your first year
Source of this problem is my Physics book from Brilliant Tutorials for IIT-JEE (the toughest engineering entrance exam in the world )

Eek, how many students can survive, let alone be inspired, when having to face with this exam? The level of this problem is a way too advanced to high school students

What is the mistake there anyway?

It's sin(theta), not cos(theta).

 

[zorro]

The question doesn't mean that you hold and release the rod at the vertical position! The rod is first held at the (theta) position, then released. The question wants us to show that right after being released, the rod will slide if the above expression is satisfied. This is why there is no centripetal acceleration included: right after being released, the rod hasn't gained any speed yet, so centripetal acceleration at that time = 0!

Thanks alot.

Eek, how many students can survive, let alone be inspired, when having to face with this exam? The level of this problem is a way too advanced to high school students

Lol. Only 8000 students of a total of 4 lakh survive ::
This is a normal problem. There are much much more tougher problems than this

 

[zorro]

The question doesn't mean that you hold and release the rod at the vertical position! The rod is first held at the (theta) position, then released. The question wants us to show that right after being released, the rod will slide if the above expression is satisfied. This is why there is no centripetal acceleration included: right after being released, the rod hasn't gained any speed yet, so centripetal acceleration at that time = 0!

If the rod hasn't gained any speed yet, why do we have an expression for tangential acceleration? Is it not 0 just after releasing?

considering the torque acting about the point of contact,
mgcos(theta) l/2=ml^2/3 (alpha)
from here,
tangential acceleration is 3gcos(theta)/4

 

[hikaru1221]

Eek, you may want to read my first sentence in post 17

 

[zorro]

right after being released, the rod hasn't gained any speed yet, so centripetal acceleration at that time = 0!

I am not talking about the centripetal acceleration. I agree that it will be 0 just after releasing.
What about tangential acceleration of the COM (perpendicular to the rod)? Is it not 0?

 

[hikaru1221]

Oh, sorry
Tangent acceleration is just like acceleration a in motion in the straight line, right? That is: for rotation, d(omega)/dt = tangent acceleration; for motion in the straight line, dv/dt = a.
Then when v=0, is a equal 0? If a = 0 when v = 0, how can the particle gain any speed at the very next second and move?

P.S.: Perhaps my words in post #17 were quite confusing. By "hasn't gained any speed yet", I meant that the rod has 0 speed before and up to the time it is released.

 

[zorro]

Ah I get it now. Thanks!