Rotational Kinetic Energy of a rod

[klopez]

1.A wooden block of mass M resting on a frictionless, horizontal surface is attached to a rigid rod of length and of negligible mass. The rod is pivoted at the other end. A bullet of mass m traveling parallel to the horizontal surface and perpendicular to the rod with speed v hits the block and becomes embedded in it.

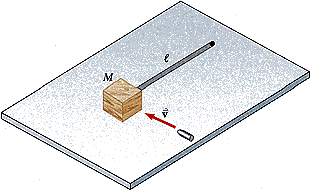
What fraction of the original kinetic energy is converted into internal energy in the collision?


Here is my attempt:

Ki = (1/2)mv^2

kf = (m+M) L^2

Now I'm a bit confused what they mean by fraction, so I initial thought I had to divide Kf/Ki , which is:

2(m + M)L^2 / (mv^2)

but WebAssign marked it wrong. I have one more try and I want to try the other way, Ki/Kf but I don't want to get it wrong.

Can anyone help me and tell me if I'm doing this right or not. Thanks

Kevin

 

[awvvu]

Your final kinetic energy equation is wrong. First off, it doesn't have the right units. It looks like you just used I. The final energy should be 1/2 I w^2, where the equation v = Lw holds.

 

[klopez]

Oh okay I see how I got the final kinetic energy wrong. I did only use I. I fixed it, and now its:

Kf = (1/2)(m + M)v^2

Can anyone confirm this?

And if that's correct, how do I find the fraction?