EEristavi
- 108
- 5
- Homework Statement
- A uniform pole is propped between the floor and the
ceiling of a room. The height of the room is 7.80 ft,
and the coefficient of static friction between the pole
and the ceiling is 0.576. The coefficient of static friction
between the pole and the floor is greater than that
between the pole and the ceiling. What is the length
of the longest pole that can be propped between the
floor and the ceiling
- Relevant Equations
- T = F R
I have a solution, However Cant understand 1 point.Now, This is the solution:
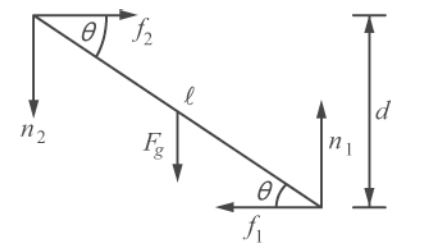
##N_2 l cos\theta + \frac 1 2 F_g l cos\theta - f_2 l sin\theta = 0##
## N_2(1 - \mu tan\theta) + \frac 1 2 F_g = 0##
This is the the point that I don't like - yes it is less that 0, but it's even less that ##\frac 1 2 F_g = 0##
## N_2(1 - \mu tan\theta) < 0 ## ?
## (1 - \mu tan\theta) < 0 ##
##tan\theta > \mu^{-1} ##
##\theta ## ≅ 60.1
l = ##\frac h {sin\theta}##Can someone please explain it to me.
##N_2 l cos\theta + \frac 1 2 F_g l cos\theta - f_2 l sin\theta = 0##
## N_2(1 - \mu tan\theta) + \frac 1 2 F_g = 0##
This is the the point that I don't like - yes it is less that 0, but it's even less that ##\frac 1 2 F_g = 0##
## N_2(1 - \mu tan\theta) < 0 ## ?
## (1 - \mu tan\theta) < 0 ##
##tan\theta > \mu^{-1} ##
##\theta ## ≅ 60.1
l = ##\frac h {sin\theta}##Can someone please explain it to me.