Satellite mechanics: linear and rotational momentum

[vasya]

Homework Statement

?

Relevant Equations

f = ma

[This is a continuation of OP's thread here: https://www.physicsforums.com/threads/satellite-mechanics-linear-and-rotational-momentum.1046963/ ]

satellite mechanics: linear and rotational momentum
I'm trying to better understand classical mechanics, and came up with a question:
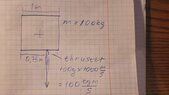
Say we have a squared satellite weighting 100kg, 1 meter on each side. it has a thruster on it's side, shown in picture
thruster quickly ejects 100g of propellant with a speed of 1000m/s giving a satellite 100kg m/s of momentum. the question is how much of it will be given to rotation, and how much - to linear motion

 

[kuruman]

How do you think you should proceed to answer your question? What assumptions must you make?

 

[vasya]

How do you think you should proceed to answer your question? What assumptions must you make?

I don't know. That's the reason I come here. I'm trying to figure out way to solve such kind of problems, because it is so generalized.

 

[haruspex]

You quoted F=ma. There is a similar equation regarding momentum. It can be obtained from F=ma by integrating wrt time.
Likewise, there is an equation for torque and angular acceleration, and integrating that wrt time gives one relating angular velocity and angular momentum.
I expect you have met all these equations.

 

[kuruman]

Figuring out how to solve such kind of problems is a worthwhile goal and you've come to right place for help. The emphasis is on help because we do not give out answers but we guide people to the answers. However, you must have some prior knowledge of the concepts behind the necessary analysis to answer your question. In short, how much you know and understand already. On one hand, it would be no help to you if we start talking about things you don't understand. On the other hand, if you don't have a basic understanding of the ideas we are talking about, we cannot provide that basic understanding; you have to acquire it on your own and then come back to us.

That said, let me ask you a few questions. Consider it homework that you have to do.

You have a cube to which an impulse Δp = 100 kg⋅m/s is delivered at the indicated point, 0.75 m from the edge. You say that the cube will translate and rotate at the same time. I agree.
Question 1. After the impulse is delivered, what quantities related to the motion of the cube are conserved and why?
Question 2: What are the mathematical expressions for the quantities that are conserved?
Question 3: Given the expressions in the previous questions, what additional quantities related to the cube need to be specified?

That is the beginning. Once you answer these questions, we will have something to refer to as we proceed to answering your question. As I was typing this, I noted that @haruspex also has some questions that you should consider answering.

 

[vasya]

>Question 1. After the impulse is delivered, what quantities related to the motion of the cube are conserved and why?
mass. total energy. Also people mentioned conservation of linear and angular momentum.
But i think that it is not the right approach to this problem, because burnt fuel cloud here should be considered a single particle. it is ejected in single quick event. not continuous. so it wont have angular momentum.
>Question 2: What are the mathematical expressions for the quantities that are conserved?
as for kinetic energy, e = 1/2*m*v^2
rotational kinetic energy e = 1/2*I*phi^2
Still not sure how it relates to my question.

 

[kuruman]

But i think that it is not the right approach to this problem, because burnt fuel cloud here should be considered a single particle. it is ejected in single quick event. not continuous. so it wont have angular momentum.

Forget the burnt fuel; it's gone, pooof!. What matters is that it changed the linear and angular momentum of the cube from zero to non-zero. The linear momentum change is already given. How do you think you should proceed to find the angular momentum change about the cube's center of mass?

 

[haruspex]

so it wont have angular momentum.

A fundamental fact about angular momentum is that it is in respect of a specified axis. A box mass m sliding along the floor at velocity v doesn’t have angular momentum about its mass centre, but it does have it about a point on the floor. In general, if the axis is at distance r from the linear path of the mass centre then the angular momentum is mvr.
So pick a convenient axis and consider the angular momenta of satellite and propellant before and after ejection.

 

[vasya]

A fundamental fact about angular momentum is that it is in respect of a specified axis. A box mass m sliding along the floor at velocity v doesn’t have angular momentum about its mass centre, but it does have it about a point on the floor. In general, if the axis is at distance r from the linear path of the mass centre then the angular momentum is mvr.
So pick a convenient axis and consider the angular momenta of satellite and propellant before and after ejection.

i didn't get it...
especially the part about a sliding box. if box is sliding, it's not rotating, so why do you speak about angular momentum?

 

[haruspex]

i didn't get it...
especially the part about a sliding box. if box is sliding, it's not rotating, so why do you speak about angular momentum?

Let's start with a point particle mass m, velocity $\vec v$ at position $\vec r$ relative to some chosen origin. Its angular momentum about the origin is $m\vec r\times\vec v$. This is definition.
If we have an assemblage of particles, a rigid body perhaps with a mass m, and its mass centre is moving with velocity $\vec v$ at position $\vec r$ relative to some chosen origin, its orbital angular momentum about the origin is $m\vec r\times\vec v$. In addition, it may have spin angular momentum about its mass centre. Its total angular momentum about the origin, i.e. the sum of its spin and orbital angular momenta, is equal to the sum of the angular momenta of the individual particles about the origin.
$\Sigma m_i=m$
$\Sigma m_i\vec r_i=m\vec r$
$\Sigma m_i\vec v_i=m\vec v$
$\vec L=\Sigma (m_i\vec r_i\times\vec v_i)$
$=(\Sigma m_i(\vec r_i-\vec r)\times(\vec v_i-\vec v))+(\Sigma m_i\vec r_i)\times\vec v+\vec r\times(\Sigma m_i\vec v_i)-(\Sigma m_i\vec r\times\vec v)$
$=(\Sigma m_i(\vec r_i-\vec r)\times(\vec v_i-\vec v))+m\vec r\times\vec v$
$=\vec L_{spin}+\vec L_{orbital}$

 

[jbriggs444]

i didn't get it...
especially the part about a sliding box. if box is sliding, it's not rotating, so why do you speak about angular momentum?

To come right out and say it: You do not need rotation to have angular momentum.

@haruspex has given you the formula for the angular momentum of a point mass about a specified reference point. @haruspex uses the three dimensional definition in which angular momentum is a [pseudo-]vector: the vector cross product of a displacement $\vec{r}$ and a velocity $\vec{v}$ which is also multiplied by mass, $m$. You do not need to worry about the "[pseudo]" part. It is irrelevant for our purposes here.

In first year physics, one normally considers angular momentum in only two dimensions. So it is taken about a chosen reference axis and is treated as a scalar with a direction (clockwise or counter-clockwise). One still takes the vector cross product. The magnitude of the cross product is given by $mrv \sin \theta$ where $\theta$ is the angle between the displacement vector and the velocity vector. The magnitude of the cross product is the same for both the two dimensional and the three dimensional definitions.

Thanks to @haruspex for correction on $\sin$ versus $\cos$.

 

[haruspex]

The magnitude of the cross product is given by $mrv \cos \theta$ where $\theta$ is the angle between the displacement vector and the velocity vector.

$mrv \sin \theta$

 

[vasya]

It's too hard to comprehend.

 

[haruspex]

It's too hard to comprehend.

You'll never handle angular momentum correctly if you don't accept that if a car mass m goes past you in a straight line at steady speed v, distance s from you at the closest, then its angular momentum about you is a constant magnitude msv.
Just take that as definition.

How does this connect with what you thought was angular momentum, the bit associated with the spin of an object?
Let's say we choose that msv as being in the positive sense, so the angular momentum is msv, not -msv.
If another car of the same mass goes at speed v in the opposite direction on a parallel line distance 2r closer (2r<s) then its angular momentum about you is m(2r-s)v. The sum of the two is 2mrv. So now it doesn’t matter where you are in the picture; the angular momentum is 2mrv about any axis in the plane. And if instead of straight lines we make them go around a circle diameter 2r, always on opposite sides, it is still 2mrv.
Populating the circle with more cars, total mass M, the angular momentum is Mrv, as you would understand for a rotating hoop.

 

[kuruman]

Here is a picture that might help you understand angular momentum. As @haruspex already mentioned in post #10, the definition of angular momentum is
$\mathbf{L}=\mathbf{r}\times\mathbf{p}=m\mathbf{r}\times\mathbf{v}.$ The magnitude (size) of angular momentum can be written as $L=mvr\sin\theta$ where $\theta$ is the angle between the position vector to the moving object and its velocity vector. Now look at the drawing below.

The plane is flying in a straight line above ground at fixed height $h$. The position of the plane relative to the base of the tree is $r$. According to the definition, the plane has orbital angular momentum $L=mvr\sin\theta=mvh$ about the base of the tree even though it is flying in a straight line. "Well", you might ask, "how can it have orbital angular momentum if it is not rotating about anything?" The answer is "But it is rotating!" Rotation involves an angle changing with time. Here angle $\theta$ is changing with respect to time and that is sufficient to establish rotation. The plane doesn't need to follow a circular path in order to be considered as orbiting the base of the tree.

 

[vasya]

ahh I got it about angular momentum...
And also I tried to simulate this problem in professional software. this is what I got:
linear velocity 1 m/s
angular velocity 1.5 rad/s
it seems like it is a violation in conservation of energy. Am I missing something?
Thanks for all of your responses!
moment of inertia=16.66

 

[jbriggs444]

ahh I got it about angular momentum...
And also I tried to simulate this problem in professional software. this is what I got:
linear velocity 1 m/s

Well, let us see. 100 kilogram satellite given 100 kg m/s of momentum. You get linear velocity of 1 m/s.

Yes. That is the correct answer.

angular velocity 1.5 rad/s

Well, let us see. The moment of inertia of a 100 kg cube that is 1 meter on a side about its center. $\frac{1}{12}m(h^2+w^2)$. Yes, that comes to 16.67 kg m², just as you have it.

The angular momentum of 100 kg m/s of linear momentum at a perpendicular offset of 0.5 meters is 50 kg m²/s. Divide by 16.67 kg m². I make that 3 inverse seconds (which means 3 rad/sec).

One of us is off by a factor of two.

it seems like it is a violation in conservation of energy. Am I missing something?

You are missing that you cannot idealize a rocket firing the way you have idealized a rocket firing.

Saying that the rocket fires "quickly" does not change the fact that the craft recoils while the rocket is still firing. If the rocket fires quickly, the craft recoils quickly. You cannot idealize this away and suppose that the same rocket delivers the same energy to the craft in all circumstances.

A rocket firing dead center on a cubical face will in fact deliver less energy to the craft than an identical rocket firing from an edge.

The extra energy for the edge case comes because the more rapidly recoiling rocket dumps less energy into the exhaust stream.

 

[Frabjous]

A rocket firing dead center on a cubical face will in fact deliver less energy to the craft than an identical rocket firing from an edge.

Would you expand on this? Is there something “deep” on why this is so? I understand the idea of recoil while the rocket is firing.

 

[jbriggs444]

Would you expand on this? Is there something “deep” on why is so? I understand the idea of recoil while the rocket is firing.

If the rocket fires dead center, the craft does not rotate. The rocket's mounting point recoils at an average speed of 0.5 m/s over the course of the impulse.

If the rocket fires on an edge, the craft does rotate. The rocket's mounting point recedes at an average of 0.5 m/s from the linear motion plus an additional 1.5 times 0.5 = 0.75 m/s (your numbers) or 3.0 times 0.5 = 1.5 m/s (my numbers) from rotation.

That difference leads to a reduction in the average exhaust velocity. Energy is conserved. If you reduce exhaust velocity for the same expenditure of chemical potential energy, you have to increase craft energy.

Or look at it from a point of view of work. The rocket delivers a fixed thrust (we assume). If that thrust is exerted while the mounting point moves a long distance, a lot of work is done. If that thrust is exerted while the mounting point moves a short distance, a little work is done.

 

[vasya]

so how to resolve it?

 

[jbriggs444]

so how to resolve it?

How to resolve what? What conflict do you perceive?

Edit: A 100 kg m/s impulse can deliver a different amount of energy to a 100 kg object depending on where it is applied. That is simply a fact of mechanics.

 

[vasya]

conflict is that we have 10000 N burst lasting 0.01s on input, 100 kg*m/s of linear momentum and additional 1.5rad/sec of angular velocity on output. 1.5rad/sec*16.66= 25 units of angular momentum. 100 on input, 125 on output

 

[jbriggs444]

conflict is that we have 10000 N burst lasting 0.01s on input, 100 kg*m/s of linear momentum and additional 1.5rad/sec of angular velocity on output. 1.5rad/sec*16.66= 25 units of angular momentum. 100 on input, 125 on output

You are adding linear momentum to angular momentum and expecting the total to be conserved?!

Linear and angular momentum are conserved separately. Not as a sum. They do not share the same units! Adding them together would yield a meaningless result since it would have no particular units.

Linear momentum: 100 kg m/s in. 100 kg m/s out. Conserved.
Angular momentum: 50 kg m²/s in. 3 rad/sec * 16.67 kg m² out = 50 units of angular momentum out. Conserved.

 

[vasya]

The angular momentum of 100 kg m/s of linear momentum at a perpendicular offset of 0.5 meters is 50 kg m2/s. Divide by 16.67 kg m2.

offset from what?

 

[haruspex]

offset from what?

Offset from the reference axis. If an object moving in a straight line passes at distance s from the reference axis then s is its perpendicular offset.

 

[vasya]

ok. in this case angular momentum is calculated by that formula. according to it angular momentum is really conserved. thanks for your help and attention. So I have 2/3 of angular momentum in linear and 1/3 in rotary motion. Bot why exactly proportion is that?

 

[haruspex]

ok. in this case angular momentum is calculated by that formula. according to it angular momentum is really conserved. thanks for your help and attention. So I have 2/3 of angular momentum in linear and 1/3 in rotary motion. Bot why exactly proportion is that?
View attachment 318965

How did you determine that ratio? Are you assuming the satellite has uniform density?

 

[vasya]

Are you assuming the satellite has uniform density?

yes I am

 

[jbriggs444]

ok. in this case angular momentum is calculated by that formula. according to it angular momentum is really conserved. thanks for your help and attention. So I have 2/3 of angular momentum in linear and 1/3 in rotary motion. Bot why exactly proportion is that?

By my calculations, initial angular momentum is zero and final angular momentum is zero as well. Angular momentum is conserved after all.

The initial angular momentum consists of two parts.

1. Unburnt rocket fuel sitting motionless in a rocket pod.

2. A motionless craft.

The final angular momentum consists of two [or three after an edit] parts.

1. An expanding plume of rocket exhaust of unknown mass and velocity that has 100 kg m/s of linear momentum at an offset of 0.5 meters from the craft's center of mass for a total of -50 kg m²/s.

2. A rotating craft with a rotation rate of 3 rad/s and a moment of inertia of 16.67 kg m^2/s for a total of +50 kg m²/s.

[3. A moving craft with an offset of 0 meters from the reference axis and, thus, zero angular momentum from its linear motion]

I adopt a reference axis at the center of the craft. Other possibilities exist and result in different numbers for angular momentum. However angular momentum is conserved regardless of the choice of axis, as long as that axis is inertial.

Where do you see 1/3 and 2/3?

 

[haruspex]

2/3 of angular momentum in linear and 1/3 in rotary motion.

As explained, what angular momentum results from linear motion depends on the choice of axis. If you choose an axis on the line of motion of the mass centre then it does not contribute any angular momentum.
What axis are you using here?

 

[vasya]

If you choose an axis on the line of motion of the mass centre then it does not contribute any angular momentum

it does. A rotary one. Moment of inertia*angular velocity

 

[haruspex]

it does. A rotary one. Moment of inertia*angular velocity

No, I wrote that the linear motion would not contribute to the angular momentum about that axis.
Please post the details of your calculation that arrives at 1/3 and 2/3.

 

[jbriggs444]

*shudder*. I think I see it. 100 kg m/s of linear momentum and 50 kg m²/s of angular momentum from rotation. He is taking the ratio of two quantities which have different units and pretending that the result is a dimensionless two to one ratio.

Naturally, the linear momentum is also 10,000 kg cm/s of linear momentum and 500,000 kg cm²/s of angular momentum from rotation for an equally defensible one to fifty ratio. "Equally defensible" because neither is at all defensible as a dimensionless ratio.

Two per meter and one per fifty centimeters are both the same ratio. Both have units.

 

[haruspex]

*shudder*. I think I see it. 100 kg m/s of linear momentum and 50 kg m²/s of angular momentum from rotation. He is taking the ratio of two quantities which have different units and pretending that the result is a dimensionless two to one ratio.

Naturally, the linear momentum is also 10,000 kg cm/s of linear momentum and 500,000 kg cm²/s of angular momentum from rotation for an equally defensible one to fifty ratio. "Equally defensible" because neither is at all defensible as a dimensionless ratio.

One half per meter and one per fifty centimeters are both the same ratio. Both have units.

Yes, that's probably the blunder. I was thrown by

angular momentum in linear … motion

taking that mean the linear momentum's contribution to angular momentum.

 

[vasya]

An expanding plume of rocket exhaust of unknown mass and velocity that has 100 kg m/s of linear momentum at an offset of 0.5 meters from the craft's center of mass for a total of -50 kg m2/s.

look more closely on first picture in this thread. thruster has offset of 0.25m of y-piersing-through-the-center-of-mass axis