Scale factors in spherical coordinates

Click For Summary
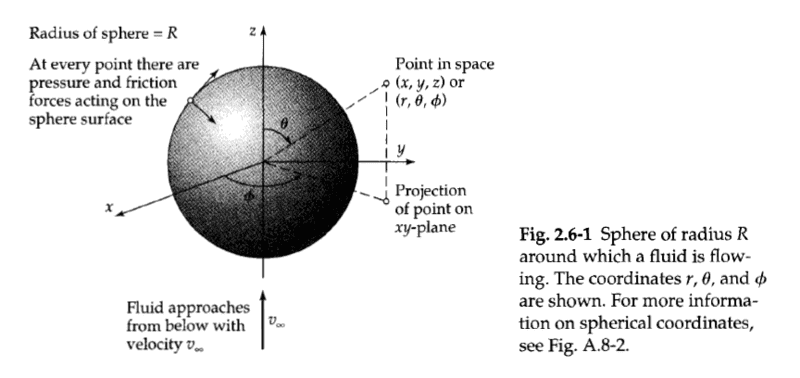
The discussion focuses on the derivation of scale factors in spherical coordinates, specifically how the value for the scale factors h is determined. The scale factors are essential for converting between Cartesian and spherical coordinate systems, impacting calculations in various fields such as physics and engineering. The document referenced provides a detailed explanation of the mathematical relationships involved in this conversion. Key points include the significance of the radial distance, polar angle, and azimuthal angle in defining these scale factors. Understanding these scale factors is crucial for accurate modeling and analysis in three-dimensional space.
Est120
Messages
54
Reaction score
3
Homework Statement
how they get that result
Relevant Equations
Geometric relations
how they got that value for the scale factors h?
1622304452773.png
1622304486479.png
 
Physics news on Phys.org

Thread 'Help with derivation of electric field of a moving charge'

At first, I derived that: $$\nabla \frac 1{\mu}=-\frac 1{{\mu}^3}\left((1-\beta^2)+\frac{\dot{\vec\beta}\cdot\vec R}c\right)\vec R$$ (dot means differentiation with respect to ##t'##). I assume this result is true because it gives valid result for magnetic field. To find electric field one should also derive partial derivative of ##\vec A## with respect to ##t##. I've used chain rule, substituted ##\vec A## and used derivative of product formula. $$\frac {\partial \vec A}{\partial t}=\frac...
View full post »

Similar threads

Electrodynamics: Dirac Delta function and Gauss' divergence theorem
Replies
6
Views
1K
Reverse engineering formulas for directing a plane wave
Replies
5
Views
2K
Method of Images, combination of an infinite plane and a hemisphere
Replies
10
Views
3K
Deriving the Laplacian in spherical coordinates
Replies
9
Views
4K
How Do You Calculate the Electric Potential of an Ellipsoid?
Replies
4
Views
2K
How to Solve the Laplace Equation for Potential Flow Around a Sphere?
Replies
1
Views
1K
Find the field inside and outside a spherical geometry
Replies
2
Views
2K
Boundary condition for a flow past a spherical obstacle
Replies
12
Views
2K
How to calculate a sink using spherical coordinates
Replies
7
Views
1K
Heat transfer: Temperature distribution inside a sphere submerged in a fluid
Replies
13
Views
3K