School Projectile Motion Problem

[jaysinghrath]

If a point of the parabolic path the velocity be u and the inclination to the horizon be θ, at what time the particle is moving at right angle to its former direction.
I was trying to solve it using vectors.
My friend gave me a clue of applying some geometry to the parabolic path given below:-

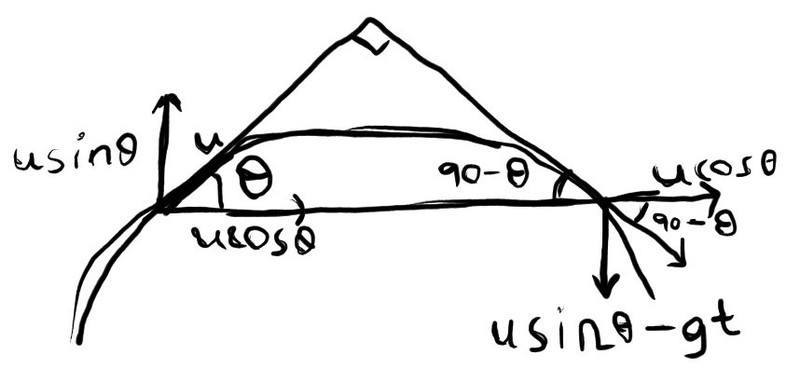
He is definite that he solver it and the answer is = ucosec(θ)/g which is matching with the answer solving via vectors. Now he is not in contact, I was trying to solve this question.
PLZ help me

 

[voko]

You are required by the forum's rules to show your attempt to get help here.

 

[gneill]

If you recall your functions classes, a line perpendicular to a line with slope m has slope - 1/m. What 's the slope of the line tangent to the first point on your diagram? So what should be the slope of the second point?

Can you write another expression for the slope at the second point?