Sensor - Calculate the Capacitance

[2013]

Homework Statement

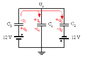
Airbag Sensor
To trigger the airbag, accelerometers are used.
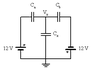
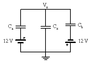
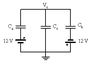
A simple sensor is composed of three parallel plates of the surface A, which are connected to a condenser system.
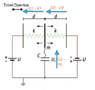
The mass m of the middle plate can move between the two fixed outer
Moving plates. She is stopped by two identical k, isolated springs of spring constants. The springs are not stressed when the plate is in the center.


To what maximum distance x, the middle plate
is deflected, when the vehicle is braked suddenly from movement at a constant acceleration a.

Determine how large the additional capacitance C must be when the airbag to trigger a voltage Uc = 0.15 V and this needs to happen at a speed of 10 ms ^ -2.
To use the values ​​d = 1.0 cm, A = 250 cm2, m = 50 g, k = 5.0 × 102 N m ^ -1 and U = 12 V.

2. The attempt at a solution

x(t)=x0e−δt cos(ωt+φ)

x(t)= F(t)/D

C2 -C1 ≈∆d/d


Is it right what I have done?
What should I do now? How can I calculate the additional capacitance C ?

 

[2013]

It would be very nice if somebody could help me.
To make to clearer for you how the sensor looks like I have got a picture of it.

 

[gneill]

What is the reasoning behind your solution attempt? What does it mean to set a difference in capacitances to a pure number (ratio of distances)?

Can you list the things you need to accomplish in order to solve the problem?

 

[2013]

differential equation (Accelerating force generated):
m*d^{2}/dt^{2}+k*dx/dt+Dx = F(t) = m*a(t)

damped harmonic oscillation:
x(t)=xo*e−δt cos(ωt*φ)

when the force or acceleration slower is than the time constant (T=2π/w):
x(t)= F(t)/D

through F=m*a:
F=D*x
a= D/m * x

Is it right?
How can I calculate the capacitance?

 

[gneill]

You won't need the differential equation for the spring-mass system; Use conservation of energy to find the maximum displacement after the constant acceleration is suddenly applied.

For the capacitance, what is the capacitance given plate area and separation of plates?

For the electrical part of the problem, start simple and assume that the sensor consists of two capacitors, C_a and C_b. Find an expression for the potential across the unknown capacitor C_x in terms of C_a and C_b. Later you can plug in expressions or values for C_a and C_b.

 

[2013]

F(x)=-kx
U(x)=∫(0-x) F(x) dx = 0,5k*x^2
E=T+U=const.

Q=C*U
W=0,5C*U^2

Is it right? How should I go on?

 

[gneill]

F(x)=-kx
U(x)=∫(0-x) F(x) dx = 0,5k*x^2
E=T+U=const.

Sure, the total energy is constant. So write an expression for the current mechanical system. Find the maximum displacement given the applied acceleration.

Hint: The applied acceleration is equivalent to a gravitational field... imagine a vertical spring with a mass on the end held there at the spring's relaxed position. Then the mass is released. The "gravitational" acceleration acting is the applied acceleration a rather than g. What's the lowest position the mass will reach relative to its initial position? The concepts of conservation of potential and kinetic energy apply.

Q=C*U
W=0,5C*U^2

Is it right? How should I go on?

You haven't written the expression for the capacitance of a capacitor given the plate area and separation. Once you do, write expressions for both variable capacitors given a displacement from the rest position, Δx.

You have to solve the circuit for the potential across the unknown capacitor. Start with assigning variables C_a and C_b to the two variable capacitors; you can worry about their actual values later.

 

[2013]

W=Fg*∆x=m*g*∆x
∆x=W/m*g

C=ԑ*A/d
∆C=Cb-Ca=ԑA/d±∆d - ԑA/d = ±ԑA*∆d/d*(d±∆d) = ±Ca*∆d/d±∆d

 

[2013]

Is this right?
How should I go on?

 

[gneill]

W=Fg*∆x=m*g*∆x
∆x=W/m*g

I don't see the spring constant in there. I see g rather than a. g does not come into play in this problem, I only drew a comparison with a spring and mass in a gravitational field as an analogous example. Use a for acceleration. What is W in terms of the given values (spring constant, mass)?

C=ԑ*A/d
∆C=Cb-Ca=ԑA/d±∆d - ԑA/d = ±ԑA*∆d/d*(d±∆d) = ±Ca*∆d/d±∆d

The formula for capacitance is right. But rather than ∆C, work out the capacitance values of the individual sections. The sensor has three plates, which translates into two capacitors in series (C_a, C_b) The unknown capacitor C_x is connected where the two sensor capacitors join.

Is this right?
How should I go on?

You still need to complete the expression for the displacement distance Δd in terms of the spring constant, the mass, and the acceleration. Leaving a new variable, W, in the expression is not useful.

You still need to analyze the circuit to determine the voltage across the unknown capacitor V_x in terms of the two varying capacitors C_a and C_b.

 

[2013]

∆d=k/m*aCa=ԑA/d-∆d
Cb=ԑA/d+∆d
Ua=Uo/2 * ∆d/d

Is it right? And then?

 

[gneill]

∆d=k/m*a

What units does your expression yield? Check your derivation. Also use parentheses when order of operations is ambiguous. Is your expression (k/m)*a, or k/(m*a)?

Ca=ԑA/d-∆d
Cb=ԑA/d+∆d
Ua=Uo/2 * ∆d/d

Is it right? And then?

I have no idea what Ua or Uo are. What's Vx in terms of C_a, C_b, C_x?

Surely you can work out some strategy to move forward if you have Δd and expressions for the capacitors and the voltage Vx? What conditions have to be met?

 

[2013]

∆d=k/(m*a)
k[N/m]; m[g]; a[m/s^2]

Is it right? I am not sure with the units.

Vx=Vo/2 * ∆d/d

 

[gneill]

∆d=k/(m*a)
k[N/m]; m[g]; a[m/s^2]

Is it right? I am not sure with the units.

Multiply out and reduce the units for your expression. You've got the right units for the individual variables (keep in mind that the Newton is a composite unit itself -- kg*m*s^-2).

Vx=Vo/2 * ∆d/d

You'll have to explain how you arrived at the above. What's Vo?

 

[2013]

[kg*m/s^2] : [m] : [kg * m/s^2] = [kg] : [m] : [kg] =m

I think the formula is right.?

Uo is an alternating voltage is applied to this circuit, the voltage drop V1
to a resistor equal to Vo / 2
Is in the left stitch V2=Vo * Zc2/(Zc1+Zc2) of the complex resistance Z=(iwC)^-1 of the capacitors. This results in the output voltage according to some equivalence transformations Va=V1-V2=Vo/2 * (C2-C1)/(C2+C1) with the capacity Ca=ԑA/d-∆d and Cb=ԑA/d+∆d it follows after another equivalence transformation:
Vx=Vo/2 * ∆d/d

Is it right? How should I go on?

 

[gneill]

[kg*m/s^2] : [m] : [kg * m/s^2] = [kg] : [m] : [kg] =m

I think the formula is right.?

kg/m/kg yields 1/m.

The equation is inverted. Better check your derivation steps.

Uo is an alternating voltage is applied to this circuit, the voltage drop V1
to a resistor equal to Vo / 2
Is in the left stitch V2=Vo * Zc2/(Zc1+Zc2) of the complex resistance Z=(iwC)^-1 of the capacitors. This results in the output voltage according to some equivalence transformations Va=V1-V2=Vo/2 * (C2-C1)/(C2+C1) with the capacity Ca=ԑA/d-∆d and Cb=ԑA/d+∆d it follows after another equivalence transformation:
Vx=Vo/2 * ∆d/d

Here's your circuit:

There's no alternating voltage source in the circuit, and no resistors... just two 12V DC supplies and three capacitors. You'll probably want to use the capacitor voltage division rule and superposition to analyze the circuit. Here's the same circuit rearranged slightly with the capacitors made obvious:

 

[2013]

I have really no idea, what I have to do.
I know: C=Ca+Cx+Cb
V=V1=V2...

Could you please help me?

 

[gneill]

I have really no idea, what I have to do.
I know: C=Ca+Cx+Cb
V=V1=V2...

No, the capacitors are not in parallel; the voltage sources are separating their lower connections.

Could you please help me?

I think you'll have to review your circuit analysis classwork. We can't just solve the problem for you; you must make a realistic attempt and we can then offer suggestions or point out errors.

As I mentioned previously, you might want to look at superposition and the capacitor voltage divider rule.

 

[2013]

V=(Vc*Cc)/C
Cc=(V*C)/Vc

C=εo*εr*A/d
d=k/(m*a)

Cc=(V*εo*εr*(A/k/(m*a)))/Vc

Is this right?
What have I do wrong?

 

[gneill]

V=(Vc*Cc)/C
Cc=(V*C)/Vc

What do the variables in the above pertain to? What does the first expression describe?

C=εo*εr*A/d
d=k/(m*a)

The dielectric in the capacitor is assumed to be air, with a dielectric constant pretty much indistinguishable from 1.00, so no need to introduce an εr here. And as we discussed previously, your formula for Δd is inverted --- it yields 1/Δd. It doesn't yield the capacitor separation, it yields the CHANGE in its separation from its rest position. One capacitor's separation gets smaller by Δd, the other gets larger by Δd.

Cc=(V*εo*εr*(A/k/(m*a)))/Vc

Is this right?
What have I do wrong?

We still need to see a correct circuit analysis for the 3 capacitors and 2 voltage supplies. If you were given only the circuit which I posted in post #10, what expression would you derive for the voltage Vx?

 

[2013]

The total voltage required is equal to voltage times the total capacity required by capacitance.


Cc = (V*ԑA/d±∆d - ԑA/d)/Vc = (V * ԑA/d * ±(k/(m*a)) - ԑA/d) / Vc

Is it right?

 

[gneill]

The total voltage required is equal to voltage times the total capacity required by capacitance.


Cc = (V*ԑA/d±∆d - ԑA/d)/Vc = (V * ԑA/d * ±(k/(m*a)) - ԑA/d) / Vc

Is it right?

I don't recognize the concept "total capacity required by capacitance", it doesn't make sense to me. Perhaps it's just me misunderstanding your intention?

The formula you've written for Cc doesn't look correct either. Is Cc meant to be the unknown central capacitor? Why not begin by writing the expression for the node voltage V_c in terms of C_a, C_b, C_c, and the 12V supplies? Put aside the expressions for C_a and C_b for now and just use the symbols C_a and C_b. Here's the circuit again using your choice of variable names:

 

[2013]

I'm sorry, but I have no idea anymore.
I am having difficulty understanding your aid because English is not my native language.
Can you please give me your approach expressed in a formula?

 

[gneill]

My suggested approach involves two concepts. The first is the superposition principle whereby you can analyze a circuit by considering only one source at a time while the others are suppressed, then summing the the results. You should have seen this method and used it in basic circuit theory class. If not, you can research it online and find it explained with examples. Here's an example.

The second concept is that of voltage division by capacitors in series. Since components in series share the same current, the charge on two capacitors in series must be equal. Thus, if you know the total voltage across the capacitor string you can find the charge on both capacitors and thus the individual voltages on the two capacitors. If C1 and C2 are two capacitors in series and there's a total voltage V across them, then the voltage on capacitor C1 is:
$$V_{C1} = V \frac{C2}{C1 + C2}$$

 

[2013]

I think I have to search C1.
This information I have given: VC = 0,15 V; a=10 m s−2; d = 1,0 cm; A = 250 cm2; m = 50 g;
k = 5,0 · 102 Nm−1 and V = 12 V

so I have this formula C1=V*(C2/Vc1)-C2

Is it right?

 

[gneill]

I think I have to search C1.
This information I have given: VC = 0,15 V; a=10 m s−2; d = 1,0 cm; A = 250 cm2; m = 50 g;
k = 5,0 · 102 Nm−1 and V = 12 V

so I have this formula C1=V*(C2/Vc1)-C2

Is it right?

The formula is correct for a voltage divider consisting of two capacitors, C1 and C2.

Your circuit is slightly more complex. You need to analyze the circuit to find an expression for the center capacitor Cc according to your given criteria.

 

[2013]

The following applies:
C1=εo*A/(do+∆d) C2=εo*A/(do-∆d)

For the difference between the two capacities gives:
∆C=C2-C1=2* εo*A*∆d/(do^2-(∆d)^2)

linear relationship between acceleration and measuring voltage results:
V(d)=-Vo/2 * m/(k*d) * a

Is it right?
I have no other idea anymore.
Please help me. I have to solved this problem, unfortunately we have not dealt with this issue in the classroom. If I do not get solved the problem, I fall through. I hope you can help me?

 

[gneill]

The following applies:
C1=εo*A/(do+∆d) C2=εo*A/(do-∆d)

For the difference between the two capacities gives:
∆C=C2-C1=2* εo*A*∆d/(do^2-(∆d)^2)

Why are you taking the difference between the two capacities?

You have a circuit with three capacitors and two 12V voltage sources. You need to solve the circuit to determine the voltage on the third capacitor (the unknown capacitor in the middle) given that you know the values of the other two capacitors. Then you rearrange the equation to solve for the unknown capacitance in terms of its voltage and the other capacitors. The required voltage on the third capacitor is given to you as the trigger potential.

As I suggested before, apply superposition and capacitor voltage division to analyze the circuit.

Separately, you can calculate actual values for the two sensor capacitors from the given mechanical situation (The Δd that results from the given acceleration sets the values of the two capacitors). Plug those two values into the expression obtained from the circuit analysis to yield the value of the unknown capacitor.

linear relationship between acceleration and measuring voltage results:
V(d)=-Vo/2 * m/(k*d) * a

Is it right?

I can't tell. What is Vo?

I have no other idea anymore.
Please help me. I have to solved this problem, unfortunately we have not dealt with this issue in the classroom. If I do not get solved the problem, I fall through. I hope you can help me?

I can only continue to restate the hints and suggestions I've given. So far you've managed to correctly find expressions for the two sensor capacitors in terms of Δd. You have also made good progress on analyzing the plate movement, but I haven't seen an actual value for Δd calculated.

Once you have that numerical value for Δd you can find numerical values for the two capacitors that make up the sensor. After that it's circuit analysis as I described to find the unknown capacitor value using the now known capacitor values and the given trigger potential across that unknown capacitor.

 

[2013]

Okay this is my idea:
C1 = ԑo * A/(d+∆x) = ԑo * A/(d+(m*a/k)) = 8,854*10^-12 * 0,025m/0,01m+(0,05kg*10m/s^2 / 5*10^2N/m)
= 2,01*10^-11As/V
C2 = ԑo * A/(d-∆x) = 2,46*10^-11As/V

Cges = (C1 · C2) / (C1+C2) = 1,107*10^-11As/V

Q = V * C =12V * 1,107*10^-11As/V = 1,33 * 10^-11As
C = Q / Vc = 1,33 * 10^-11As / 0,15V = 8,854*10^-10As/V

Is it right?
Have you got the solution? Tomorrow I have to present it and I have no idea

 

[gneill]

Okay this is my idea:
C1 = ԑo * A/(d+∆x) = ԑo * A/(d+(m*a/k)) = 8,854*10^-12 * 0,025m/0,01m+(0,05kg*10m/s^2 / 5*10^2N/m)
= 2,01*10^-11As/V
C2 = ԑo * A/(d-∆x) = 2,46*10^-11As/V

Okay, those values for the capacitance of the sensor sections look okay. Note that the units As/V is equivalent to Coulomb/Volt, which is also commonly called Farads. So your capacitances are C1 = 24.6 pF and C2 = 20.1 pF, with pF being picofarads.

Cges = (C1 · C2) / (C1+C2) = 1,107*10^-11As/V

I'm not sure why you're paralleling the two capacitors of the sensor. Can you explain your reasoning?

Q = V * C =12V * 1,107*10^-11As/V = 1,33 * 10^-11As
C = Q / Vc = 1,33 * 10^-11As / 0,15V = 8,854*10^-10As/V

Is it right?
Have you got the solution? Tomorrow I have to present it and I have no idea

Your value for for the unknown capacitor doesn't look right. Can you explain your approach to analyzing the circuit?